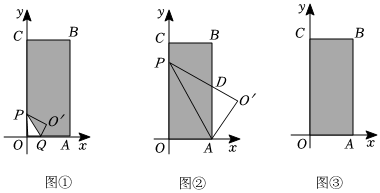
將一個矩形紙片OABC放置在平面直角坐標(biāo)系中，點O（0，0），點A（3，0），點C（0，6）．
（1）如圖①，點P在邊OC上，（點P不與O、C重合），折疊該紙片，使折痕所在的直線經(jīng)過點P，并與x軸的正半軸相交于點Q，且∠OPQ=30°，點O的對應(yīng)點O′落在第一象限，設(shè)OQ=t,則∠O′QA的大小為 60°60°，并用含有字母t的式子表示點O′的坐標(biāo)為 （32t,32t）（32t,32t）；
（2）如圖②，若P在邊OC上一點，沿AP翻折得到新△APO′，且PO′交AB邊于點D，若△PAD面積為5110．
①求PD長；
②求P點坐標(biāo)；
（3）如圖③，點E是AB的中點，點F在BC邊上，且CF=1．若M為x軸上的動點，N為y軸上的動點，則四邊形MNFE的周長最小值為 97+1397+13（直接寫出結(jié)果）．
3
2
3
2
3
2
3
2
51
10
97
13
97
13
【考點】四邊形綜合題．
【答案】60°；（t，t）；+
3
2
3
2
97
13
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：247引用：2難度：0.1
相似題
-
1．如圖1，數(shù)軸上A，C兩點表示的數(shù)分別是a,c,BD∥AC，設(shè)BD=b,且（a-2）2+|b-1|=0，b+c＜0．
（1）求a,b的值；
（2）E為線段AC上的動點，連接BE，∠ABE和∠DBE的平分線分別交直線AC于點F，G，∠DBG和∠BAC的平分線交于點H，且∠BAC=60°，∠DBF=k∠BHA．
①求k的值；
②如圖2，DO⊥AC，垂足為O，將四邊形ABDC沿射線DO方向平移h（h＞0）個單位得到四邊形A'B'D'C'，其中A'B'，D'C'分別交數(shù)軸于點M，N，若AN+CM=，且圖中陰影部分面積為32k，則h的值是 （直接寫出答案，無需證明）．34-32c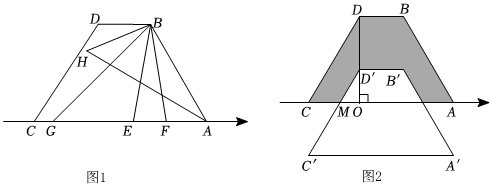
發(fā)布：2025/6/8 1:0:1組卷：23引用：2難度：0.1 -
2．閱讀與應(yīng)用：同學(xué)們：你們已經(jīng)知道（a-b）2≥0，即a2-2ab+b2≥0．
∴a2+b2≥2ab（當(dāng)且僅當(dāng)a=b時取等號）．
閱讀1：若a,b為實數(shù)，且a＞0，b＞0，∵（-a）2≥0，∴a-2b+b≥0．ab
∴a+b≥2（當(dāng)且僅當(dāng)a=b時取等號）．ab
閱讀2：若函數(shù)y=x+（m＞0，x＞0，m為常數(shù)），由閱讀1結(jié)論可知：mx
x+≥2mx即x+x?mx≥2mx，m
∴當(dāng)x=，即x2=m,∴x=mx（m＞0）時，函數(shù)y=x+m的最小值為2mx．m
閱讀理解上述內(nèi)容，解答下列問題：
問題1：若函數(shù)y=a-1+（a＞1），則a=時，函數(shù)y=a-1+16a-1（a＞1）的最小值為 ；16a-1
問題2：已知一個矩形的面積為9cm,求此矩形周長的最小值；
問題3：求代數(shù)式（m＞-1）的最小值．m2+2m+10m+1發(fā)布：2025/6/7 23:30:2組卷：59引用：1難度：0.2 -
3．如圖，四邊形ABCD是正方形，點O為對角線AC的中點．
（1）問題解決：如圖①，連接BO，分別取CB，BO的中點P，Q，連接PQ，則PQ與BO的數(shù)量關(guān)系是 ，位置關(guān)系是 ；
（2）問題探究：如圖②，△AO'E是將圖①中的△AOB繞點A按順時針方向旋轉(zhuǎn)45°得到的三角形，連接CE，點P，Q分別為CE，BO'的中點，連接PQ，PB．判斷△PQB的形狀，并證明你的結(jié)論；
（3）拓展延伸：如圖③，△AO'E是將圖①中的△AOB繞點A按逆時針方向旋轉(zhuǎn)45°得到的三角形，連接BO'，點P，Q分別為CE，BO'的中點，連接PQ，PB．若正方形ABCD的邊長為1，求△PQB的面積．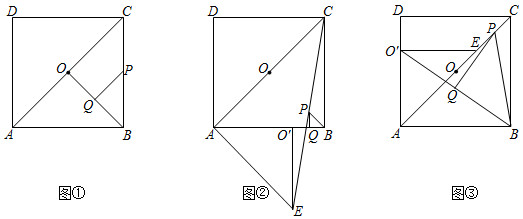
發(fā)布：2025/6/8 0:0:1組卷：2547引用：16難度：0.2
相關(guān)試卷