請(qǐng)閱讀下列材料，完成相應(yīng)的任務(wù)：
羅狄斯托勒密（Claudius Ptolemaeus,約90年168年），“地心說”的集大成者，生于埃及，著名的天文學(xué)家，地理學(xué)家、占星學(xué)家和光學(xué)家．
托勒密定理實(shí)出自依巴谷（Hipparchus）之手，托勒密從他的書中摘出并加以完善．
托勒密定理：圓的內(nèi)接四邊形兩對(duì)對(duì)邊乘積的和等于兩條對(duì)角線的乘積．
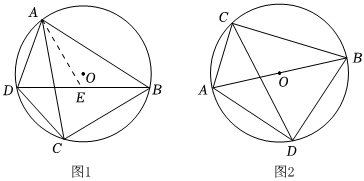
如圖1，四邊形ABCD內(nèi)接于⊙O，求證：AB?CD+BC?AD=AC?BD
下面是該結(jié)論的證明過程：
證明：如圖1，作∠BAE=∠CAD，交BD于點(diǎn)E．∵?AD=?AD，∴∠ABE=∠ACD（依據(jù)1），∴△ABE∽△ACD（依據(jù)2），∴ABAC=BECD，∴AB?CD=AC?BE，∵?AB=?AB，∴∠ACB=∠ADE，∵∠BAE=∠CAD，∴∠BAE+∠EAC=∠CAD+∠EAC，即∠BAC=∠EAD，…
任務(wù)：
（1）托勒密定理的逆命題是 如果一個(gè)四邊形兩對(duì)對(duì)邊乘積的和等于兩條對(duì)角線的乘積，那么這個(gè)四邊形是圓的內(nèi)接四邊形如果一個(gè)四邊形兩對(duì)對(duì)邊乘積的和等于兩條對(duì)角線的乘積，那么這個(gè)四邊形是圓的內(nèi)接四邊形；上述證明過程中的“依據(jù)1”為 同弧所對(duì)的圓周角相等同弧所對(duì)的圓周角相等；依據(jù)2”為 兩個(gè)角分別對(duì)應(yīng)相等的兩個(gè)三角形相似兩個(gè)角分別對(duì)應(yīng)相等的兩個(gè)三角形相似；
（2）請(qǐng)完成后續(xù)證明；
（3）如圖2，以AB為直徑的⊙O中，點(diǎn)C為⊙O上一點(diǎn)，且∠ABC=30°，∠ACB的角平分線交⊙O于點(diǎn)D，連接AD，BD，若AB=4，求CD的長(zhǎng)．
?
AD
=
?
AD
AB
AC
=
BE
CD
?
AB
?
AB
【考點(diǎn)】圓的綜合題．
【答案】如果一個(gè)四邊形兩對(duì)對(duì)邊乘積的和等于兩條對(duì)角線的乘積，那么這個(gè)四邊形是圓的內(nèi)接四邊形；同弧所對(duì)的圓周角相等；兩個(gè)角分別對(duì)應(yīng)相等的兩個(gè)三角形相似
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：606引用：2難度：0.4
相似題
-
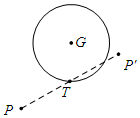1．對(duì)于平面內(nèi)點(diǎn)P和⊙G，給出如下定義：T是⊙G上任意一點(diǎn)，點(diǎn)P繞點(diǎn)T旋轉(zhuǎn)180°后得到點(diǎn)P'，則稱點(diǎn)P'為點(diǎn)P關(guān)于⊙G的旋轉(zhuǎn)點(diǎn)．如圖為點(diǎn)P及其關(guān)于⊙G的旋轉(zhuǎn)點(diǎn)P'的示意圖．
在平面直角坐標(biāo)系xOy中，⊙O的半徑為1，點(diǎn)P（0，-2）．
（1）在點(diǎn)A（-1，0），B（0，4），C（2，2）中，是點(diǎn)P關(guān)于⊙O的旋轉(zhuǎn)點(diǎn)的是 ；
（2）若在直線y=x+b上存在點(diǎn)P關(guān)于⊙O的旋轉(zhuǎn)點(diǎn)，求b的取值范圍；
（3）若點(diǎn)D在⊙O上，⊙D的半徑為1，點(diǎn)P關(guān)于⊙D的旋轉(zhuǎn)點(diǎn)為點(diǎn)P'，請(qǐng)直接寫出點(diǎn)P'的橫坐標(biāo)xP′的取值范圍．
發(fā)布：2025/6/12 8:30:1組卷：547引用：3難度：0.1 -
2．如圖，四邊形ABCD內(nèi)接于⊙O，AC為對(duì)角線，AC=AD，直徑AE交CD于點(diǎn)F，連接DE．
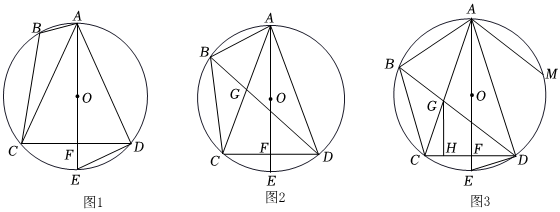
（1）如圖1，求證：AE⊥CD；
（2）如圖2，連接BD交AC于點(diǎn)G，∠AGD+∠ADC=180°，求證：；?BC=?CD
（3）如圖3，在（2）的條件下，過點(diǎn)G作GH⊥CD于H，過點(diǎn)A作AM∥BD交⊙O于點(diǎn)M，若BG=GH，AE=10，求線段AM的長(zhǎng)．發(fā)布：2025/6/12 9:0:1組卷：66引用：5難度：0.3 -
3．如圖1，在直角梯形ABCD中，AD∥BC，∠A=90°，AB=8cm,AD=6cm,BC=10cm.點(diǎn)P從點(diǎn)B出發(fā)沿BD方向勻速運(yùn)動(dòng)，速度為1cm/s；同時(shí)，線段EF從CD出發(fā)沿DA方向勻速運(yùn)動(dòng)，速度為1cm/s,且EF與BD交于點(diǎn)Q，連接PE、PF．當(dāng)點(diǎn)P與點(diǎn)Q相遇時(shí)，所有運(yùn)動(dòng)停止．若設(shè)運(yùn)動(dòng)時(shí)間為t（s）．
（1）求CD的長(zhǎng)度；
（2）當(dāng)PE∥AB時(shí)，求t的值；
（3）①設(shè)△PEF的面積為S，求S關(guān)于t的函數(shù)關(guān)系式；
②如圖2，當(dāng)△PEF的外接圓圓心O恰好在EF中點(diǎn)時(shí)，則t的值為（請(qǐng)直接寫出答案）發(fā)布：2025/6/12 9:0:1組卷：143引用：2難度：0.5
相關(guān)試卷