【問題情境】
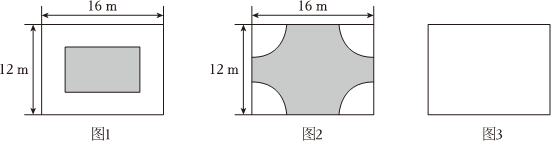
在一塊長16m,寬12m的矩形荒地上，建造一個花園，要求花園所占面積為荒地面積的一半．方案一：如圖1，花園四周小路的寬度相等；方案二：如圖2，矩形中每個角上的扇形相同．
【數學思考】
（1）求方案一中小路的寬度，設小路的寬度為x米，請列出方程，并解答；
（2）求方案二中扇形的半徑；（其中π≈3，結果保留根號）
【知識遷移】
（3）你還有其他的設計方案嗎？請在圖3中畫出你的設計草圖，并將花園部分涂上陰影．
【考點】四邊形綜合題．
【答案】（1）2m；
（2）；
（3）圖案見解答過程．
（2）
4
2
m
（3）圖案見解答過程．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/9/17 2:0:9組卷：32引用：1難度：0.2
相似題
-
1．如圖，點P是正方形ABCD對角線AC上一動點，點E在射線BC上，且PE=PB，連接PD，O為AC中點．
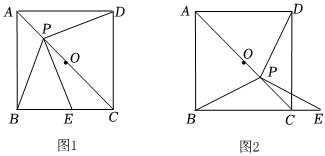
（1）如圖1，當點P在線段OA上時，試猜想PE與PD的數量關系和位置關系．
（2）如圖2，當點P在線段OC上時，（1）中的猜想還成立嗎？請說明理由．
（3）如圖2，試用等式來表示PB、BC、CE之間的數量關系：．發布：2025/6/8 18:0:1組卷：53引用：1難度：0.1 -
2．按要求回答下列問題：
發現問題．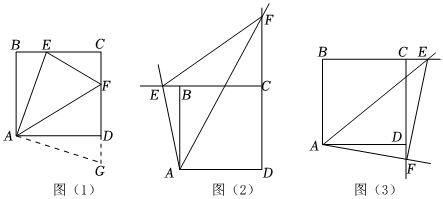
（1）如圖（1），在正方形ABCD中，點E，F分別是BC，CD邊上的動點，且∠EAF=45°，易證：EF=DF+BE．（不必證明）；
（2）類比延伸
①如圖（2），在正方形ABCD中，如果點E，F分別是邊BC，CD延長線上的動點，且∠EAF=45°，則（1）中的結論還成立嗎？請寫出證明過程；
②如圖（3），如果點E，F分別是邊BC，CD延長線上的動點，且∠EAF=45°，則EF，BE，DF之間的數量關系是 ．（不要求證明）
（3）拓展應用：如圖（1），若正方形的ABCD邊長為6，，求EF的長．AE=35發布：2025/6/8 18:30:1組卷：235引用：4難度：0.1 -
3．定義：四邊形ABCD中，將對角線AC和BD的平方和，即AC2+BD2的值稱為四邊形ABCD的“特征數”．
（1）①在菱形ABCD中，AB=4，∠BAD=60°，則菱形ABCD的“特征數”=；
②正方形EFGH的“特征數”等于16，則邊長=；
（2）平行四邊形ABCD中，AB=a,BC=b,試證明：平行四邊形ABCD的“特征數”為2a2+2b2；
（3）利用（2）的結論解決下列問題：
平行四邊形ABCD中，，BC=6，且AC?BD=60，AC＜BD，試求AC和BD的長度．AB=42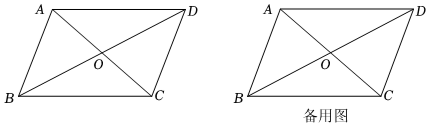
發布：2025/6/8 15:0:1組卷：373引用：3難度：0.2