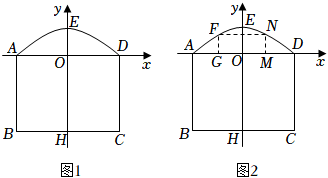
如圖1所示為某公司生產的A型活動板房，成本是每個395元，它由長方形和拋物線構成，長方形的長AD=4米，寬AB=3米，拋物線的最高點E到BC的距離為4米．
（1）按如圖1所示建立平面直角坐標系；求該拋物線的解析式．
（2）現將A型活動板房改為B型活動板房．如圖2，在拋物線與AD之間的區域內加裝一扇長方形窗戶框架FGMN，點G、M在AD上，點N、F在拋物線上，長方形窗戶框架的成本為10元/米，設M（m,0），且滿足12≤m≤1，當窗戶框架FGMN的周長最大時，每個B型活動板房的成本是多少？（每個B型活動板房的成本=每個A型活動板房的成本+一扇長方形窗戶框架FGMN成本）
（3）根據市場調查，以單價600元銷售（2）中窗戶框架周長最大時的B型活動板房，每月能售出100個，而單價每降低10元，每月能多售出20個．不考慮其他因素，公司將銷售單價n（元）定為多少時，每月銷售B型活動板房所獲利潤W（元）最大？最大利潤是多少？
1
2
【考點】二次函數的應用．
【答案】（1）該拋物線的函數表達式為 y=-x2+1；
（2）每個B型活動板房的成本是450元；
（3）公司將銷售單價n定為 550 元時，每月銷售B型活動板房所獲利潤W最大，最大利潤20000元．
1
4
（2）每個B型活動板房的成本是450元；
（3）公司將銷售單價n定為 550 元時，每月銷售B型活動板房所獲利潤W最大，最大利潤20000元．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：231引用：2難度：0.4
相似題
-
1．有一種產品的質量分成6種不同檔次，若工時不變，每天可生產最低檔次的產品40件；如果每提高一個檔次，每件利潤可增加1元，但每天要少生產2件產品．
（1）若最低檔次的產品每件利潤17元時，生產哪一種檔次的產品的利潤最大？并求最大利潤．
（2）由于市場價格浮動，生產最低檔次的產品每件利潤可以從8元到24元不等，那么生產哪種檔次的產品所得利潤最大？發布：2025/5/27 19:30:1組卷：128引用：3難度：0.1 -
2．吉林省某大學的校門是一拋物線形水泥建筑物，大門的地面寬度為8米，兩側距P地面4米高處各有一個掛校名橫匾用的鐵環，兩鐵環的水平距離為6米，則校門的高為（精確到0.1米，水泥建筑物厚度忽略不計）（ ）發布：2025/5/27 18:0:1組卷：507引用：10難度：0.5 -
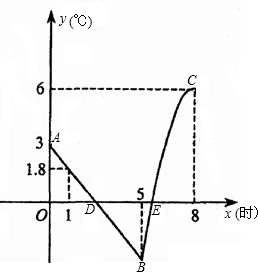3．春、秋季節，由于冷空氣的入侵，地面氣溫急劇下降到0℃以下的天氣現象稱為“霜凍”．由霜凍導致植物生長受到影響或破壞現象稱為霜凍災害．某種植物在氣溫是0℃以下持續時間超過3小時，即遭到霜凍災害，需采取預防措施．下圖是氣象臺某天發布的該地區氣象信息，預報了次日0時～8時氣溫隨著時間變化情況，其中0時～5時的圖象滿足一次函數關系，5時～8時的圖象滿足二次函數y=-x2+mx+n關系．請你根據圖中信息，解答下列問題：
（1）求次日5時的氣溫；
（2）求二次函數y=-x2+mx+n的解析式；
（3）針對這種植物判斷次日是否需要采取防霜措施，并說明理由．（參考數據：≈2.45）6發布：2025/5/28 1:0:2組卷：156引用：12難度：0.1