【初識模型】
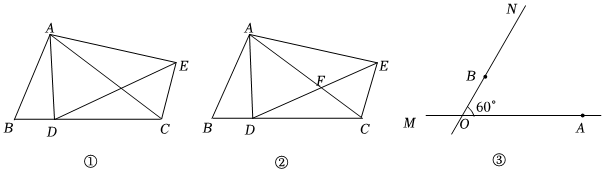
（1）如圖①，在△ABC中，D是BC上一點，∠B=∠ACE，ABAC=BDCE，連接DE．
求證：（Ⅰ）ABAC=ADAE；
（Ⅱ）∠B=∠ADE．
【再研模型】
（2）如圖②，在△ABC中，D是BC上一點，∠B=∠ADE=∠ACE．求證：ABAC=BDCE．
【應用模型】
（3）如圖③，直線AM與BN交于點O，∠AOB=60°，一輛快車和一輛慢車分別從A，B兩處沿AM，BN方向同時勻速行駛，快車速度是慢車速度的2倍，在行駛過程中兩車與某一定點P所組成的三角形的形狀始終不變．當兩車距離為700m時，慢車到定點P的距離為 10071007m.
AB
AC
=
BD
CE
AB
AC
=
AD
AE
AB
AC
=
BD
CE
7
7
【考點】相似形綜合題．
【答案】100
7
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：1133引用：3難度：0.4
相似題
-
1．在△ABC中，AB=AC，∠BAC=90°，點D，E分別是AC，BC的中點，點P是射線DE上一點，連接AP，將線段PA繞點P順時針旋轉90°得到線段PM，連接AM，CM．
（1）如圖①，當點P與點D重合時，線段CM與PE的數量關系是 ，∠ACM=°；
（2）如圖②當點P在射線DE上運動時（不與點D，E重合），求的值；PECM
（3）連接PC，當△PCM是等邊三角形時，請直接寫出的值．ACCM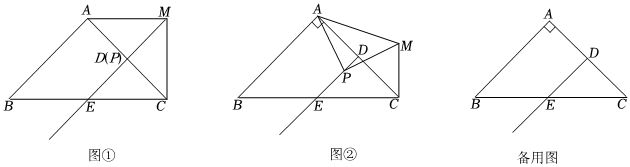
發布：2025/5/23 0:30:1組卷：370引用：2難度：0.1 -
2．如圖1，已知正方形AFEG與正方形ABCD有公共頂點A，點E在正方形ABCD的對角線AC上（AG＜AD）．
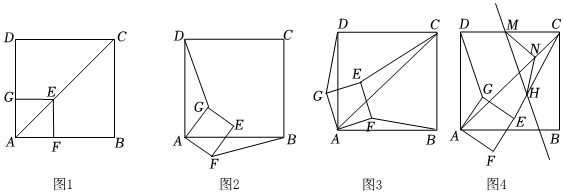
（1）如圖2，正方形AFEG繞A點順時針方向旋轉α（0°＜α＜90°），DG和BF的數量關系是 ，位置關系是 ；
（2）如圖3，正方形AFEG繞A點逆時針方向旋轉α（0°＜α＜90°），求的值以及直線CE和直線DG所夾銳角的度數；CEDG
（3）如圖4，AB=8，點N在對角線AC上，CN=，將正方形AFEG繞A順時針方向旋轉α（0°＜α＜360°），點M是邊CD的中點，過點M作MH∥DG交EC于點H；在旋轉過程中，線段NH的長度是否變化？如果不變，請直接寫出NH的長度；如果改變，請說明理由．22發布：2025/5/22 23:30:1組卷：682引用：1難度：0.3 -
3．已知矩形ABCD，點E為直線BD上的一個動點（點E不與點B重合），連接AE，以AE為一邊構造矩形AEFG（A，E，F，G按逆時針方向排列），連接DG．
（1）如圖1，當=ADAB=1時，請直接寫出線段BE與線段DG的數量關系與位置關系；AGAE
（2）如圖2，當=ADAB=2時，請猜想線段BE與線段DG的數量關系與位置關系，并說明理由；AGAE
（3）如圖3，在（2）的條件下，連接BG，EG，分別取線段BG，EG的中點M，N，連接MN，MD，ND，若AB=，∠AEB=45°，請直接寫出△MND的面積．5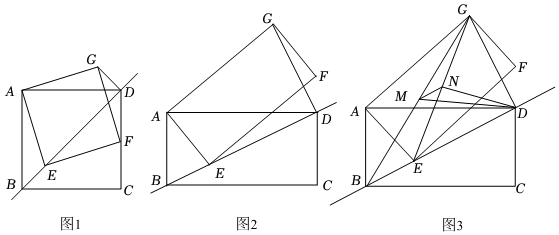
發布：2025/5/22 23:30:1組卷：2941引用：6難度：0.1