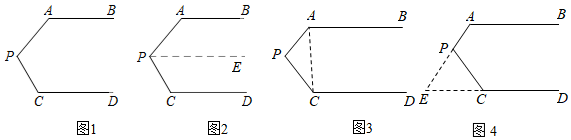
問題情境：如圖1，AB∥CD，∠PAB=130°，∠PCD=120°，求∠APC度數．
思路點撥：
小明的思路是：如圖2，過P作PE∥AB，通過平行線性質，可分別求出∠APE、∠CPE的度數，從而可求出∠APC的度數；
小麗的思路是：如圖3，連接AC，通過平行線性質以及三角形內角和的知識可求出∠APC的度數；
小芳的思路是：如圖4，延長AP交DC的延長線于E，通過平行線性質以及三角形外角的相關知識可求出∠APC的度數．
問題解決：請從小明、小麗、小芳的思路中任選一種思路進行推理計算，你求得的∠APC的度數為110110°；
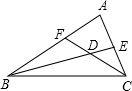
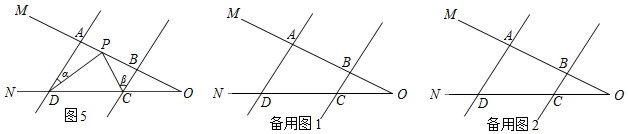
問題遷移：（1）如圖5，AD∥BC，點P在射線OM上運動，當點P在A、B兩點之間運動時，∠ADP=∠α，∠BCP=∠β．∠CPD、∠α、∠β之間有何數量關系？請說明理由；
（2）在（1）的條件下，如果點P在A、B兩點外側運動時（點P與點A、B、O三點不重合），請你直接寫出∠CPD、∠α、∠β間的數量關系．
【答案】110
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/12/23 11:0:1組卷：575難度：0.5
相似題
-
1．我們將內角互為對頂角的兩個三角形稱為“對頂三角形”．例如，在圖1中，△AOB的內角∠AOB與△COD的內角∠COD互為對頂角，則△AOB與△COD為“對頂三角形”，根據三角形內角和定理知“對頂三角形”有如下性質：∠A+∠B=∠C+∠D．
（1）如圖1，在“對頂三角形”△AOB與△OOD中，∠AOB=70°，則∠C+∠D=°．
（2）如圖2，在△ABC中，AD、BE分別平分∠BAC和∠ABC，若∠C=60°，∠ADE比∠BED大6°，求∠BED的度數．
發布：2025/5/24 11:0:1組卷：826引用：3難度：0.5 -
2．如圖，∠C=∠A=90°，∠B=25°，則∠D的度數是（ ?。?/h2>發布：2025/5/24 13:30:2組卷：831引用：5難度：0.6 -
3．如圖所示，能利用圖中作法：過點A作BC的平行線，證明三角形內角和是180°的原理是（ ?。?/h2>發布：2025/5/24 10:0:2組卷：112引用：3難度：0.7