當前位置：
試題詳情
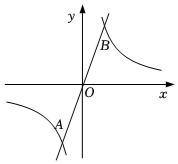如圖，反比例函數y1=k1x和正比例函數y2=k2x的圖象交于A（-1，-2）、B（1，2）兩點，若k1x＞k2x,則x的取值范圍是（ ）
k
1
x
k
1
x
【考點】反比例函數與一次函數的交點問題．
【答案】A
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/5/23 20:19:40組卷：332引用：2難度：0.8
相似題
-
1．如圖，一次函數y=kx+b與反比例函數的圖象交于A（2，4），B（-4，n）兩點．y=mx
（1）直接寫出n值和反比例函數的解析式；
（2）根據所給條件，請直接寫出不等式的解集；kx+b＞mx
（3）過點B作BC⊥x軸，垂足為C，連接AC，求S△ABC．發布：2025/5/31 14:30:1組卷：28引用：3難度：0.6 -
2．平面直角坐標系xOy中，直線y=2x與雙曲線y=
（k＞2）相交于A，B兩點，其中點A在第一象限．設M（m,2）為雙曲線y=kx（k＞2）上一點，直線AM，BM分別交y軸于C，D兩點，則OC-OD的值為（ ）kx發布：2025/5/31 15:0:2組卷：3328引用：3難度：0.4 -
3．閱讀下列材料．
定義運算：min|a,b|，當a≥b時，min|a,b|=b；當a＜b時，min|a,b|=a.例如：min|-1，3|=-1；min|-1，-2|=-2．
完成下列任務
（1）①min|（-3）0，2|=；
②=min|-14，-4|
（第25題圖）
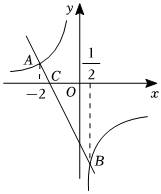
（2）如圖，已知反比例函數和一次函數y2=-2x+b的圖象交于A、B兩點．y1=kx
①當y1＜y2時，請直接寫出x的取值范圍．
②當-2＜x＜0時，．求這兩個函數的解析式．min|kx，-2x+b|=（x+1）（x-3）-x2
（3）直線AB交x軸于點C，P是x軸上的一點，若△BCP的面積是6，求點P的坐標．發布：2025/5/31 15:30:1組卷：168引用：3難度：0.6