我們知道,通過兩種不同的方法計(jì)算圖形的面積時(shí)可以一些代數(shù)恒等式.
例如,如圖1,可以得到一個(gè)代數(shù)恒等式(a+b)2=a2+2ab+b2.
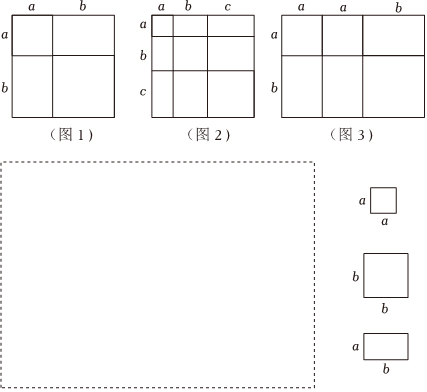
(1)仔細(xì)觀察圖2,可以得到一個(gè)代數(shù)恒等式:(a+b+c)2=a2+b2+c2+2ab+2bc+2ca(a+b+c)2=a2+b2+c2+2ab+2bc+2ca;
(2)仔細(xì)觀察圖3,可以得到一個(gè)代數(shù)恒等式:(a+b)(2a+b)=2a2+b2+3ab(a+b)(2a+b)=2a2+b2+3ab;
(3)現(xiàn)有邊長為a的正方形、邊長為b的正方形和寬、長分別為a、b的長方形紙片若干張,用它們可以拼成一個(gè)長方形,該長方形的面積滿足代數(shù)恒等式(2a+b)(a+2b)=2a2+5ab+2b2,請?jiān)诜娇蛑挟嫵鲈撻L方形(標(biāo)出相應(yīng)紙片邊長).
【答案】(a+b+c)2=a2+b2+c2+2ab+2bc+2ca;(a+b)(2a+b)=2a2+b2+3ab
【解答】
【點(diǎn)評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/7/15 8:0:9組卷:81引用:1難度:0.5
相似題
-
1.已知正整數(shù)a,b,c(其中a≠1)滿足abc=ab+8,則a+b+c的最小值是 .
發(fā)布:2025/6/7 13:30:1組卷:435引用:6難度:0.7 -
2.若a、b、c分別是三角形的3條邊的長,請判斷代數(shù)式(a-b)2-c2的值 0(填“大于”、“小于”或“等于”)
發(fā)布:2025/6/7 12:30:2組卷:150引用:2難度:0.7 -
3.先閱讀下面的內(nèi)容,再解決問題:
問題:對于形如x2+2xa+a2,這樣的二次三項(xiàng)式,可以用公式法將它分解成(x+a)2的形式.但對于二次三項(xiàng)式x2+2xa-3a2,就不能直接運(yùn)用公式了.此時(shí),我們可以在二次三項(xiàng)式x2+2xa-3a2中先加上一項(xiàng)a2,使它與x2+2xa的和成為一個(gè)完全平方式,再減去a2,整個(gè)式子的值不變,于是有:x2+2xa-3a2=(x2+2xa+a2)-a2-3a2=(x+a)2-4a2=(x+a)2-(2a)2=(x+3a)(x-a)像這樣,先添一適當(dāng)項(xiàng),使式中出現(xiàn)完全平方式,再減去這個(gè)項(xiàng),使整個(gè)式子的值不變的方法稱為“配方法”.利用“配方法”,解決下列問題:
(1)分解因式:a2-6a+5;
(2)若;a2+b2-12a-6b+45+|12m-c|=0
①當(dāng)a,b,m滿足條件:2a×4b=8m時(shí),求m的值;
②若△ABC的三邊長是a,b,c,且c邊的長為奇數(shù),求△ABC的周長.發(fā)布:2025/6/7 15:0:1組卷:525引用:3難度:0.4


