對任意一個三位數(shù)n,如果n滿足各數(shù)位上的數(shù)字互不相同,且都不為零,那么稱這個數(shù)為“相異數(shù)”,將一個“相異數(shù)”任意兩個數(shù)位上的數(shù)字對調(diào)后可以得到三個不同的新三位數(shù),把這三個新三位數(shù)的和與111的商記為F(n)。例如n=123,對調(diào)百位與十位上的數(shù)字得到213,對調(diào)百位與個位上的數(shù)字得到321,對調(diào)十位與個位上的數(shù)字得到132,這三個新三位數(shù)的和為213+321+132=666,666÷111=6,所以F(123)=6。
(1)計算:F(243),F(xiàn)(617):
(2)若s,t都是“相異數(shù)”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整數(shù)),規(guī)定:k=
F(s)F(t),當F(s)+F(t)=18時,求k的最大值。
F
(
s
)
F
(
t
)
【考點】最大與最小.
【答案】(1)9,14;
(2)。
(2)
11
7
【解答】
【點評】
聲明:本試題解析著作權屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復制發(fā)布。
發(fā)布:2024/6/27 10:35:59組卷:196引用:3難度:0.6
相似題
-
1.在圓上A、B、C、D四個位置填上4個數(shù)2,0,1,2(如圖甲),如果進行這樣的操作:每次選一個位置上的數(shù)加1,那么最少需要3次操作能達到四個位置上的數(shù)相同,操作方法有3種(C位+1,B位兩次+1;B位兩次+1,C位+1;和B位+1,C位+1,B位再+1).

現(xiàn)在如圖乙,從2,0,1,3開始,將操作方法變?yōu)槊看螌⑷齻€位置同時加1,則至少需要多少次,使之達到四個位置上的數(shù)相等.發(fā)布:2025/2/26 2:30:2組卷:24引用:1難度:0.6 -
2.用0-9這10個數(shù)字組成若干個合數(shù),每個數(shù)字都恰好用一次,那么這些合數(shù)之和的最小值是
發(fā)布:2025/2/26 0:0:1組卷:99引用:2難度:0.4 -
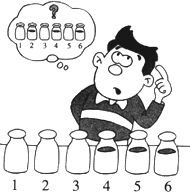 3.有三個裝有水的瓶子和三個空瓶子,排列如圖:三個裝水的瓶子和三個空瓶子分開擺.如果要把它們的排列順序變成水瓶和空瓶錯開放,一次只能挪動一個瓶子,那最少要挪動幾次?發(fā)布:2025/2/24 20:0:2組卷:12引用:1難度:0.5
3.有三個裝有水的瓶子和三個空瓶子,排列如圖:三個裝水的瓶子和三個空瓶子分開擺.如果要把它們的排列順序變成水瓶和空瓶錯開放,一次只能挪動一個瓶子,那最少要挪動幾次?發(fā)布:2025/2/24 20:0:2組卷:12引用:1難度:0.5


