如圖1，∠1、∠2是四邊形ABCD的兩個不相鄰的外角．
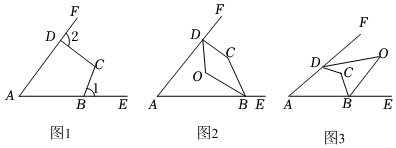
（1）猜想并說明∠1+∠2與∠A、∠C的數量關系；
（2）如圖2，在四邊形ABCD中，∠ABC與∠ADC的平分線交于點O．若∠A=58°，∠C=152°，求∠BOD的度數；
（3）如圖3，BO、DO分別是四邊形ABCD外角∠CBE、∠CDF的角平分線．請直接寫出∠A、∠C與∠O的數量關系．
【答案】（1）∠1+∠2=∠A+∠C；
（2）133°；
（3）∠C-∠A=2∠O．
（2）133°；
（3）∠C-∠A=2∠O．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：228引用：4難度：0.7
相似題
-
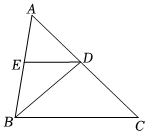1．如圖，在△ABC中，BD是∠ABC的平分線，DE∥BC交AB于點E．∠A=55°，∠BDC=95°，求∠BED的度數．發布：2025/6/11 12:30:1組卷：117引用：4難度：0.6 -
2．我們定義：
【概念理解】在一個三角形中，如果一個角的度數是另一個角度數的4倍，那么這樣的三角形我們稱之為“完美三角形”．如：三個內角分別為130°、40°、10°的三角形是“完美三角形”．
【簡單應用】如圖1，∠MON=72°，在射線OM上找一點A，過點A作AB⊥OM交ON于點B，以A為端點作射線AD，交線段OB于點C（點C不與C、B重合點）
（1）∠ABO=°，△AOB（填“是”或“不是”）“完美三角形”；
（2）若∠ACB=90°，求證：△AOC是“完美三角形”；
【應用拓展】
如圖2，點D在△ABC的邊AB上，連接DC，作∠ADC的平分線交AC于點E，在DC上取一點F，使∠EFC+∠BDC=180°，∠DEF=∠B，若△BCD是“完美三角形”，求∠B的度數．
發布：2025/6/11 12:30:1組卷：1675引用：5難度：0.6 -
3．如圖，在△ABC中，CD是AB邊上的高，CE是∠ACB的平分線．
（1）若∠A=40°，∠B=80°，求∠DCE的度數；
（2）若∠A=α，∠B=β，求∠DCE的度數（用含α、β的式子表示）．發布：2025/6/11 13:0:1組卷：581引用：7難度：0.3