為測量學校后山高度,數學興趣小組活動過程如下:
(1)測量坡角
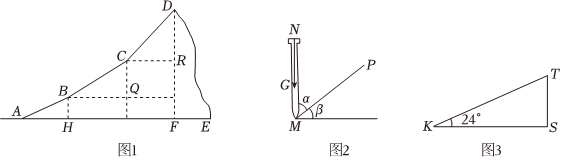
如圖1,后山一側有三段相對平直的山坡AB,BC,CD,山的高度即為三段坡面的鉛直高度BH,CQ,DR之和,坡面的長度可以直接測量得到,要求山坡高度還需要知道坡角大小.
如圖2,同學們將兩根直桿MN,MP的一端放在坡面起始端A處,直桿MP沿坡面AB方向放置,在直桿MN另一端N用細線系小重物G,當直桿MN與鉛垂線NG重合時,測得兩桿夾角α的度數,由此可得山坡AB坡角β的度數.請直接寫出α,β之間的數量關系.
(2)測量山高
同學們測得山坡AB,BC,CD的坡長依次為40米,50米,40米,坡角依次為24°,30°,45°;為求BH,小熠同學在作業本上畫了一個含24°角的Rt△TKS(如圖3),量得KT≈5cm,TS≈2cm.求山高DF.(2≈1.41,結果精確到1米)
(3)測量改進
由于測量工作量較大,同學們圍繞如何優化測量進行了深入探究,有了以下新的測量方法.
如圖4,5,在學校操場上,將直桿NP置于MN的頂端,當MN與鉛垂線NG重合時,轉動直桿NP,使點N,P,D共線,測得∠MNP的度數,從而得到山頂仰角β1,向后山方向前進40米,采用相同方式,測得山頂仰角β2;畫一個含β1的直角三角形,量得該角對邊和另一直角邊分別為a1厘米,b1厘米,再畫一個含β2的直角三角形,量得該角對邊和另一直角邊分別為a2厘米,b2厘米.已知桿高MN為1.6米,求山高DF.(結果用不含β1,β2的字母表示)
2
【答案】(1)α+β=90°;
(2)約為69米;
(3)(+1.6)米.
(2)約為69米;
(3)(
40
a
1
a
2
b
1
a
2
-
b
2
a
1
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/5/1 8:0:8組卷:879引用:3難度:0.6
相似題
-
 1.某數學興趣小組通過調查研究把“如何測量嵩岳寺塔的高度”作為一項課題活動,他們制訂了測量方案,并利用課余時間實地測量.
1.某數學興趣小組通過調查研究把“如何測量嵩岳寺塔的高度”作為一項課題活動,他們制訂了測量方案,并利用課余時間實地測量.
請你根據表中信息結合示意圖幫助該數學興趣小組求嵩岳寺塔AB的高度.課題 測量嵩岳寺塔的高度 測量工具 測量角度的儀器,皮尺等
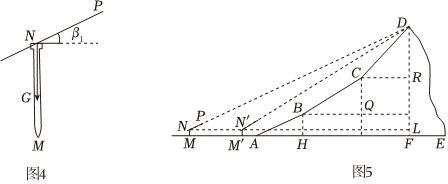
測量方案在點C處放置高為1.3米的測角儀CD,此時測得塔頂端A的仰角為45°,再沿BC方向走22米到達點E處,此時測得塔頂端A的仰角為32°. 說明:E、C、B三點在同一水平線上
(精確到0.1米,參考數據:sin32°≈0.52,cos32°≈0.84,tan32°≈0.62)發布:2025/6/6 16:30:1組卷:53引用:3難度:0.6 -
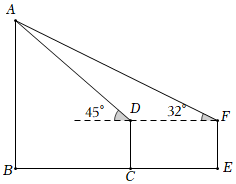
 2.如圖,學校科技小組計劃測量一處電信塔的高度,小明在A處用儀器測得塔尖D的仰角∠DAC=30°,向塔正前方水平直行260m到達點B,測得塔尖的仰角∠DBC=60°,若小明的眼睛離地面1.6m,求塔的高度.(保留一位小數.參考數據:≈1.414,2≈1.732,3≈2.236).5發布:2025/6/6 17:0:1組卷:4引用:1難度:0.4
2.如圖,學校科技小組計劃測量一處電信塔的高度,小明在A處用儀器測得塔尖D的仰角∠DAC=30°,向塔正前方水平直行260m到達點B,測得塔尖的仰角∠DBC=60°,若小明的眼睛離地面1.6m,求塔的高度.(保留一位小數.參考數據:≈1.414,2≈1.732,3≈2.236).5發布:2025/6/6 17:0:1組卷:4引用:1難度:0.4 -
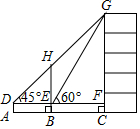 3.如圖,某數學興趣小組為測量一棵古樹BH和教學樓CG的高,先在A處用高1.5米的測角儀測得古樹頂端H的仰角∠HDE為45°,此時教學樓頂端G恰好在視線DH上,再向前走7米到達B處,又測得教學樓頂端G的仰角∠GEF為60°,點A、B、C三點在同一水平線上.
3.如圖,某數學興趣小組為測量一棵古樹BH和教學樓CG的高,先在A處用高1.5米的測角儀測得古樹頂端H的仰角∠HDE為45°,此時教學樓頂端G恰好在視線DH上,再向前走7米到達B處,又測得教學樓頂端G的仰角∠GEF為60°,點A、B、C三點在同一水平線上.
(1)計算古樹BH的高;
(2)計算教學樓CG的高.(參考數據:≈1.4,2≈1.7)3發布:2025/6/6 21:30:2組卷:2174引用:22難度:0.3
相關試卷


