設ω>0,函數(shù)f(x)=2sin(ωx-π6)+1在[π3,5π6]上單調(diào)遞減.
(1)求ω;
(2)若函數(shù)g(x)=f(x)+k在區(qū)間[-π12,5π12]上有且只有一個零點,求實數(shù)k的取值范圍.
f
(
x
)
=
2
sin
(
ωx
-
π
6
)
+
1
[
π
3
,
5
π
6
]
[
-
π
12
,
5
π
12
]
【考點】正弦函數(shù)的單調(diào)性.
【答案】(1)ω=2.
(2).
(2)
(
-
1
-
3
,-
1
+
3
]
∪
{
-
3
}
【解答】
【點評】
聲明:本試題解析著作權屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復制發(fā)布。
發(fā)布:2024/4/20 14:35:0組卷:279引用:2難度:0.5
相似題
-
1.我國著名數(shù)學家華羅庚先生曾說:數(shù)缺形時少直觀,形缺數(shù)時難入微,數(shù)形結(jié)合百般好,隔裂分家萬事休,在數(shù)學的學習和研究中,函數(shù)的解析式常用來研究函數(shù)圖象的特征,兩數(shù)
的圖象大致為( )f(x)=12x-sinxA. 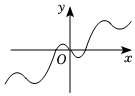
B. 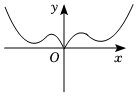
C. 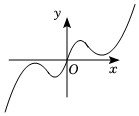
D. 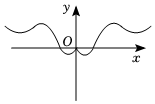 發(fā)布:2024/12/29 13:0:1組卷:182引用:4難度:0.9
發(fā)布:2024/12/29 13:0:1組卷:182引用:4難度:0.9 -
2.已知f(x)=sin(ωx+φ)(ω>0)滿足
,f(π4)=1且f(x)在f(53π)=0上單調(diào),則ω的最大值為( )(π4,5π6)A. 127B. 1817C. 617D. 3017發(fā)布:2024/12/29 11:30:2組卷:1061引用:12難度:0.7 -
3.已知函數(shù)
(ω>0)的最小正周期T=π,下列說法正確的是( )f(x)=2sin(ωx-π3)A.函數(shù)f(x)在 上是減函數(shù)[-π12,5π12]B.函數(shù)f(x)的圖象的對稱中心為 (5π12,0)C.函數(shù) 是偶函數(shù)f(x+π6)D.函數(shù)f(x)在區(qū)間 上的值域為[0,2][π6,2π3]發(fā)布:2024/12/29 12:30:1組卷:629引用:3難度:0.7


