如圖，△ABC中，AD是高，CE是中線，點G是CE的中點，DG⊥CE，點G為垂足．
（1）求證：DC=BE；
（2）若∠AEC=66°，求∠BCE的度數．
【考點】直角三角形斜邊上的中線；等腰三角形的判定與性質．
【答案】見試題解答內容
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：3511引用：17難度：0.7
相似題
-
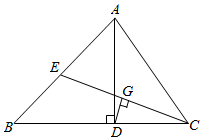1．如圖，在△ABC中，AD是BC邊上的高線，CE是AB邊上的中線，DG⊥CE于G，CD=AE．
（1）求證：CG=EG．
（2）已知BC=13，CD=5，連接ED，求△EDC的面積．發布：2024/12/23 10:0:1組卷：2026引用：13難度：0.7 -
2．我們把三角形三邊上的高產生的三個垂足組成的三角形稱為該三角形的垂足三角形．已知等腰三角形的腰長為5，底邊長為6，則該三角形的垂足三角形的周長是（ ）
發布：2024/11/22 8:0:1組卷：151引用：1難度：0.7 -
3．直角三角形的斜邊長為10cm,則斜邊上的中線長為（ ）
發布：2024/12/29 18:30:4組卷：23引用：1難度：0.7