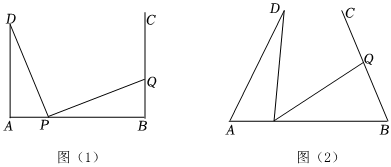
如圖（1），AB=8cm,AD⊥AB，BC⊥AB，垂足為A，B，AD=BC=6cm,點P在線段AB上以每秒2cm的速度由點A向點B運動，同時，點Q在線段BC上由點B向點C運動．連接PD，PQ，設它們運動的時間為t（s）．
（1）PA=2t2tcm,PB=（8-2t）（8-2t）cm；（用含t的代數式表示）
（2）若點Q的運動速度與點P的運動速度相等，當t=1時，判斷線段PD和線段PQ的數量關系和位置關系，并請說明理由；
（3）如圖（2），將圖（1）中的“AD⊥AB，BC⊥AB”，改為“∠DAB=∠CBA=α”，其他條件不變．設點Q的運動速度為x cm/s,當x為何值時，△ADP與△BPQ全等，請直接寫出x的值．
【考點】三角形綜合題．
【答案】2t；（8-2t）
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/4/20 14:35:0組卷：205引用：4難度：0.2
相似題
-
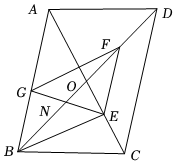1．如圖，在?ABCD中，對角線AC，BD相交于點O，BD=2AD，E，F，G分別是OC，OD，AB的中點，點N為GE與BD的交點．下列結論：①GN=NE；②AE⊥GF；③BE平分∠DBC；④EF=OC．其中必定正確的結論是（ ）發布：2025/5/24 5:30:2組卷：122引用：1難度：0.6 -
2．數學實驗是通往數學之源、數學之品、數學之用、數學之奇、數學之美、數學之謎的創造之門，小瑞同學是一位數學“小迷神”，酷愛做數學實驗，今天特邀大家和他做如下實驗，并回答相關問題：
小瑞把兩塊完全相同的三角板按圖1方式擺放，其中△ABC≌△EFD，∠BAC=∠FED=60°，BC⊥AC，ED⊥FD，AB=EF=12cm,AC在直線MN上，點A與點F重合．
（1）∠CAE=，BD=cm
（2）小瑞將三角板FDE的直角頂點D沿DA方向滑動，同時頂點F沿AN方向在射線AN上滑動，如圖2．
①當點D恰好是線段AB中點時，求∠ADF的度數．
②當點D從初始位置滑動到點A處時，求點E所經過的路徑長；
（3）在（2）中，過點D、F分別作AB、AF的垂線，兩條垂線相交于點P，連接AP，線段AP的長度是否為定值？如果是，請直接寫出結果；如果不是，請說明理由．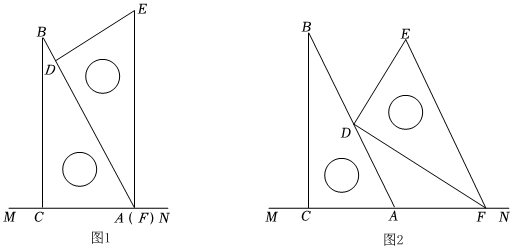
發布：2025/5/24 5:0:1組卷：287引用：1難度：0.3 -
3．【問題發現】
（1）如圖1，在等腰直角△ABC中，點D是斜邊BC上任意一點，在AD的右側作等腰直角△ADE，使∠DAE=90°，AD=AE，連接CE，則∠ABC和∠ACE的數量關系為 ；
【拓展延伸】
（2）如圖2，在等腰△ABC中，AB=BC，點D是BC邊上任意一點（不與點B，C重合），在AD的右側作等腰△ADE，使AD=DE，∠ABC=∠ADE，連接CE，則（1）中的結論是否仍然成立，并說明理由；
【歸納應用】
（3）在（2）的條件下，若AB=BC=6，AC=4，點D是射線BC上任意一點，請直接寫出當CD=3時CE的長．
發布：2025/5/24 6:30:2組卷：1340引用：12難度：0.3