一透明的敞口正方體容器ABCD-A′B′C′D′裝有液體，棱AB始終在水平桌面上，容器底部的傾斜角為α（注：圖1中∠CBE=α，圖2中BQ=3dm）．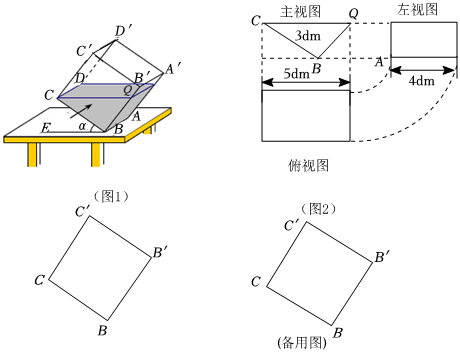
探究如圖1，液面剛好過棱CD，并與棱BB′交于點Q，其三視圖及尺寸如圖2所示，那么：
圖1中，液體形狀為 三棱柱三棱柱（填幾何體的名稱）；
利用圖2中數據，可以算出圖1中液體的體積為 2424dm3.（公式：體積=底面積×高）
拓展在圖1的基礎上，以棱AB為軸將容器向左或向右旋轉，但不能使液體溢出．若從正面看，液面與棱交于點P、Q（Q始終在棱BB′上），設PC=x,請你在圖中把此容器主視圖補充完整，并用含x的代數式表示BQ的長度．
【答案】三棱柱；24
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：346引用：2難度：0.7
相似題
-
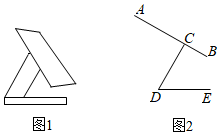1．如圖1是一種手機平板支架，圖2是其側面結構示意圖．量得托板長AB=120mm,支撐板長CD=80mm,底座長DE=90mm.托板AB固定在支撐板頂端點C處，且CB=40mm,托板AB可繞點C轉動，支撐板CD可繞點D轉動．如圖2，若∠DCB=90°，∠CDE=60°，求點A到底座DE的距離．（結果保留根號）發布：2025/6/3 2:0:7組卷：284引用：4難度：0.7 -
2．筒車是我國古代利用水力驅動的灌溉工具，唐代陳廷章在《水輪賦》中寫道：“水能利物，輪乃曲成”．如圖，半徑為3m的筒車⊙O按逆時針方向每分鐘轉
圈，筒車與水面分別交于點A、B，筒車的軸心O距離水面的高度OC長為2.2m,筒車上均勻分布著若干個盛水筒．若以某個盛水筒P剛浮出水面時開始計算時間．56
（1）經過多長時間，盛水筒P首次到達最高點？
（2）浮出水面3.4秒后，盛水筒P距離水面多高？
（3）若接水槽MN所在直線是⊙O的切線，且與直線AB交于點M，MO=8m.求盛水筒P從最高點開始，至少經過多長時間恰好在直線MN上．
（參考數據：cos43°=sin47°≈，sin16°=cos74°≈1115，sin22°=cos68°≈1140）38
發布：2025/6/3 5:0:1組卷：887引用：7難度：0.5 -
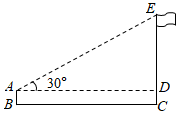3．如圖，小明利用一個銳角是30°的三角板測操場旗桿的高度，已知他與旗桿之間的水平距離BC為15m,AB為1.5m（即小明的眼睛與地面的距離），那么旗桿的高度是（ ）發布：2025/6/3 5:0:1組卷：2707引用：18難度：0.6