定義：到三角形的兩條邊的距離相等的點，叫做這個三角形的雅實心，例：如圖1，當P在△ABC的AC邊上時，若PD⊥BC于點D，PE⊥AB于點E，且PD=PE，則稱點P為△ABC的AC邊上的雅實心．△ABC各邊上的雅實心構成的新的三角形，叫做雅實三角形．
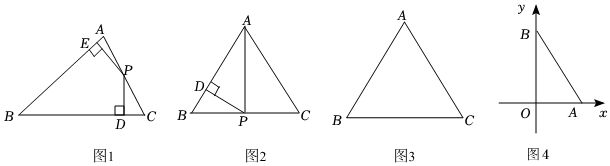
（1）如圖2，△ABC中，AB=AC=10cm,BC=12cm,求BC邊上的雅實心P到AB的距離PD的長．
（2）如圖3，等邊△ABC的邊長為4cm,求等邊△ABC的雅實三角形的面積．
（3）如圖4，在平面直角坐標系xOy中，點A，B分別在x,y軸上，且A（2，0），∠BAO=60°，求△AOB的各邊上的雅實心P的坐標．
【考點】三角形綜合題．
【答案】（1）cm；（2）cm2；（3-，3-），（0，），（4-6，0）．
24
5
3
3
3
2
3
3
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/29 23:30:1組卷：472引用：4難度：0.3
相似題
-
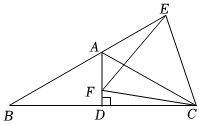1．如圖，等腰△ABC中，AB=AC，∠BAC=120°，AD⊥BC于點D，點E在BA的延長線上，點F在線段AD上，且EF=FC．有下面四個結論：
（1）AB=2AD；
（2）△AEF≌△ACF；
（3）△EFC是等邊三角形；
（4）FA+AE=EC．
其中所有正確結論的序號是 ．發布：2025/5/30 21:0:1組卷：210引用：2難度：0.5 -
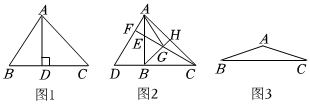2．定義：連接三角形的一個頂點和其對邊上一點，若所得線段能將該三角形分割成一個等腰三角形和一個直角三角形，則稱該線段為原三角形的“妙分線”．
（1）如圖1，在△ABC中，AB=，AD⊥BC，D為垂足，AD為△ABC的“妙分線”．若BD=1，則CD長為 ；5
（2）如圖2，在△ABC中，∠ABC=90°，AB=BC，D是CB延長線上一點，E為AB上一點，BE=BD，連接CE并延長交AD于點F，BH平分∠ABC，分別交CF，AC于點G，H，連接AG．求證：AG是△AFC的“妙分線”；
（3）如圖3，在△ABC中，AB=AC=5，BC=3．若AC為△BCD的“妙分線”，直接寫出CD的長．10發布：2025/5/30 20:0:1組卷：438引用：6難度：0.1 -
3．在等邊△ABC中，D為射線BC上一點，CE是∠ACB外角的平分線，∠ADE=60°，EF⊥BC于F．
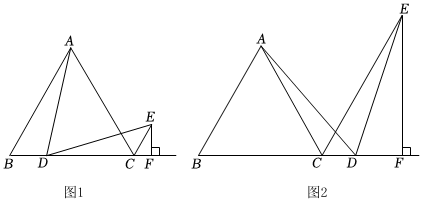
（1）如圖1，求證：CE∥AB；
（2）如圖1，若點D在線段BC上（不與B，C點重合），求證：BC=DC+2CF；
（3）如圖2，若點D在線段BC的延長線上，（2）中的結論是否仍然成立？請說明理由．發布：2025/5/30 20:0:1組卷：737引用：3難度：0.2