如圖，點B、E、C在一條直線上，線段AB=CD，AB∥CD．
（1）尺規作圖：在線段BC上取一點F，連接AF，使得△ABF≌△DCE；
（2）根據已知及（1）中你的作圖條件證明△ABF≌△DCE．
【答案】（1）作圖見解析部分；
（2）證明見解析部分．
（2）證明見解析部分．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/5/24 9:30:2組卷：84引用：1難度：0.5
相似題
-
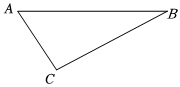1．如圖Rt△ABC中，∠ACB=90°．
（1）利用尺規作圖，作⊙C，使它與AB相切于點D、與AC相交于點E．（保留作圖痕跡，不寫作法）；
（2）在（1）的基礎上，若BC=3，∠A=60°，求弧DE的長．發布：2025/5/24 12:30:1組卷：19引用：1難度：0.5 -
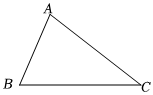2．如圖，已知△ABC，請用尺規作圖法在BC上找一點D，使得AD=CD．（保留作圖痕跡，不寫作法）發布：2025/5/24 13:30:2組卷：210引用：2難度：0.7 -
3．下面是小立設計的“過圓上一點作這個圓的切線”的尺規作圖過程．
已知：⊙O及圓上一點A．
求作：直線AB，使得AB為⊙O的切線，A為切點．
作法：如圖2，
①連接OA并延長到點C；
②分別以點A，C為圓心，大于長為半徑作弧，兩弧交于點D（點D在直線OA上方）；12AC
③以點D為圓心，DA長為半徑作⊙D；
④連接CD并延長，交⊙D于點B，作直線AB．
直線AB就是所求作的直線．
根據小立設計的尺規作圖過程，完成下面的證明．（說明：括號里填推理的依據）
證明：連接AD．
∵=AD
∴點C在⊙D上，
∴CB是⊙D的直徑．
∴=90°．（ ）
∴AB⊥．
∵OA是⊙O的半徑，
∴AB是⊙O的切線．（ ）發布：2025/5/24 14:0:2組卷：475引用：10難度：0.5