如圖1和圖2，點A在數軸上對應的數為16，過原點O在數軸的上方作射線OB，且tan∠AOB=43．點E從點A出發，沿數軸以每秒2個單位長度的速度向點O運動，同時點F從點O出發，沿OB方向以每秒1個單位長度的速度運動，當點E到達點O時，點E，F都停止運動．以點F為圓心，OF為半徑的半圓與數軸正半軸交于點C，與射線OB交于點D，連接DE，設運動時間為t秒（t＞0），點E在數軸上對應的數為x.
（1）用含t的式子表示OC的長為 65t65t，當點E與點C重合時，x=66；
（2）若DE與半圓F相切，求x；
（3）如圖2，當t=103時，半圓F與DE的另一個交點為G，猜想線段OG與GE的數量關系，并說理；
（4）若半圓F與線段DE只有一個公共點，直接寫出x的取值范圍．
tan
∠
AOB
=
4
3
6
5
6
5
t
=
10
3
【考點】圓的綜合題．
【答案】t；6
6
5
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：80引用：1難度：0.2
相似題
-
1．我們不妨定義：一組對邊平行且一組對角互余的四邊形稱為“求真四邊形”．
（1）如圖1，四邊形ABCD是“求真四邊形”，AD∥BC，若∠A=α（α＜90°），請用含α的代數式表示∠D；
（2）如圖2，AB是半圓O的直徑，點C、D、E在半圓上（點C、D、E按逆時針排列），AC，BE相交于點F．若∠DCA=∠CBE，求證：四邊形DEFC是“求真四邊形”；
（3）在（2）的條件下，連接DF，已知，若∠CDF為直角，求tan∠DCF的值．tan∠ABE=13發布：2025/6/4 17:30:2組卷：142引用：2難度：0.4 -
2．如圖，在△ABC中，∠C=90°，AD是∠BAC的平分線，O是AB上的一點，以OA為半徑的⊙O經過點D，過點D作DE⊥AB于點E．
（1）求證：△ADC≌△ADE；
（2）求證：BC是⊙O的切線；
（3）若BD=5，DC=3，求AC的長．發布：2025/6/4 14:0:1組卷：192引用：3難度：0.4 -
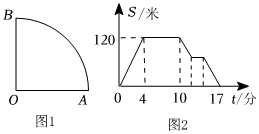3．李大爺在如圖1所示扇形湖畔的棧道上散步，他從圓心O出發，沿O→A→B→O勻速運動，最后回到點O，其中路徑AB是一段長180米的圓弧．李大爺離出發點O的直線距離S（米）與運動時間t（分）之間的關系如圖2所示．
（1）在 時間段內，李大爺離出發點O的距離在增大；在4～10分這個時間段內，李大爺在 路段上運動（填OA、AB或OB）；李大爺從點O出發到回到點O一共用了 分鐘；
（2）扇形線道的半徑是 米，李大帶的速度為 米/分；
（3）在與出發點O距離75米處有一個報刊亭，已知李大爺在買報紙前后始終保持運動速度不變，則李大爺是在第 分到達報利亭，他在報刊亭停留了 分鐘．發布：2025/6/4 16:30:1組卷：19引用：1難度：0.3