請(qǐng)閱讀下面文字并完成相關(guān)任務(wù)．
勾股定理，是幾何學(xué)中一顆光彩奪目的明珠，被稱為“幾何學(xué)的基石”．在我國(guó)最早對(duì)勾股定理進(jìn)行證明的是三國(guó)時(shí)期吳國(guó)的數(shù)學(xué)家趙爽．
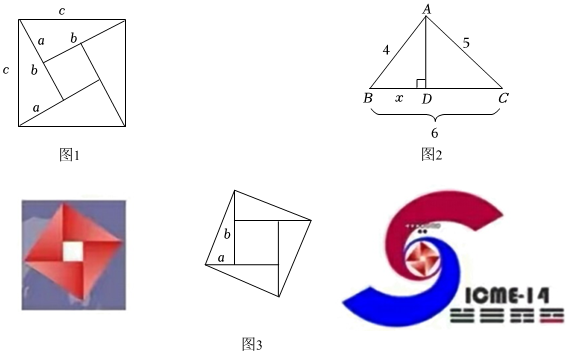
（1）如圖1是著名的趙爽弦圖，由四個(gè)全等的直角三角形拼成，用它可以驗(yàn)證勾股定理，思路是：大正方形的面積有兩種求法，一種是等于c2，另一種是等于四個(gè)直角三角形與一個(gè)小正方形的面積之和，即12ab×4+（b-a）2，從而得到等式c2=12ab×4+（b-a）2，化簡(jiǎn)便得結(jié)論a2+b2=c2．這里用兩種求法來(lái)表示同一個(gè)量從而得到等式或方程的方法，我們稱之為“雙求法”．現(xiàn)在，請(qǐng)你用“雙求法”解決下面問(wèn)題：
如圖2，在△ABC中，AD是BC邊上的高，AB=4，AC=5，BC=6，設(shè)BD=x,求x的值．
?
（2）2002年在北京召開的國(guó)際數(shù)學(xué)家大會(huì)會(huì)標(biāo)和2021年在上海召開的國(guó)際數(shù)學(xué)教育大會(huì)會(huì)標(biāo)，都包含了趙爽的弦圖．如圖3，如果大正方形的面積為18，直角三角形中較短直角邊長(zhǎng)為a,較長(zhǎng)直角邊長(zhǎng)為b,且a2+b2=ab+10，那么小正方形的面積為 22．
（3）勾股定理本身及其驗(yàn)證和應(yīng)用過(guò)程都體現(xiàn)了一種重要的數(shù)學(xué)思想是 DD．
A．函數(shù)思想
B．整體思想
C．分類討論思想
D．?dāng)?shù)形結(jié)合思想
1
2
ab
×
4
+
（
b
-
a
）
2
1
2
ab
×
4
+
（
b
-
a
）
2
【考點(diǎn)】勾股定理的證明．
【答案】2；D
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/10/19 8:0:2組卷：300引用：2難度：0.5
相似題
-
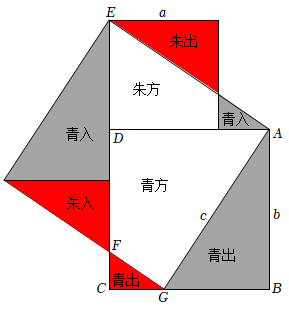
1．我國(guó)是最早了解勾股定理的國(guó)家之一，東漢末年數(shù)學(xué)家劉徽在為《九章算術(shù)》作注中依據(jù)割補(bǔ)術(shù)而創(chuàng)造了勾股定理的無(wú)字證明“青朱出入圖”，移動(dòng)幾個(gè)圖形就直觀地證明了勾股定理，如圖，若a=3，b=4，則△CFG的面積為 ．
發(fā)布：2025/5/26 4:0:1組卷：110引用：1難度：0.6 -
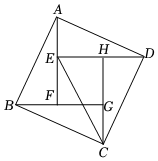2．如圖是我國(guó)漢代數(shù)學(xué)家趙爽在注解《周辭算經(jīng)》時(shí)給出的“趙爽弦圖”，它是由四個(gè)全等的直角三角形與中間的小正方形EFGH拼成的一個(gè)大正方形ABCD．連結(jié)CE，若CE=AD，則tan∠BCE的值為（ ）發(fā)布：2025/5/26 6:30:2組卷：371引用：1難度：0.3 -
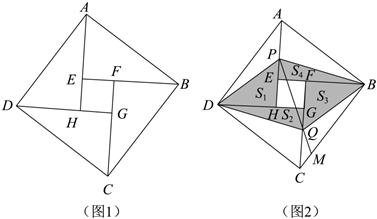
3．如圖（1）是我國(guó)古代數(shù)學(xué)家趙爽用來(lái)證明勾股定理的弦圖示意圖，圖（2）中，在線段AE和CG上分別取點(diǎn)P和點(diǎn)Q，使AP=CQ，連接PD、PB、QD和QB，則構(gòu)成了一個(gè)“壓扁”的弦圖．“壓扁”的弦圖（四邊形PBQD）中，4個(gè)直角三角形的面積（如圖（2）中的陰影部分）依次記作S1，S2，S3，S4，連接PQ并延長(zhǎng)交BC于點(diǎn)M．若AE=3EF=3，S1=S3=S2+S4，則CM的長(zhǎng)為（ ）
發(fā)布：2025/5/26 9:30:1組卷：312引用：2難度：0.4