【背景介紹】勾股定理是幾何學中的明珠,充滿著魅力.千百年來,人們對它的證明趨之若鶩,其中有著名的數學家,也有業余數學愛好者.向常春在1994年構造發現了一個新的證法.
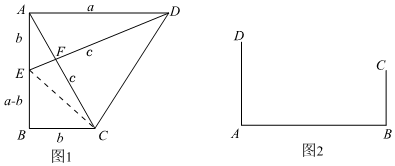
【小試牛刀】把兩個全等的直角三角形△ABC和△DAE如圖1放置,其三邊長分別為a,b,c.顯然,∠DAB=∠B=90°,AC⊥DE.請用a,b,c分別表示出梯形ABCD,四邊形AECD,△EBC的面積:
S梯形ABCD= 12a(a+b)12a(a+b);
S△EBC= 12b(a-b)12b(a-b);
S四邊形AECD= 12c212c2;
再探究這三個圖形面積之間的關系,它們滿足的關系式為 12a(a+b)=12b(a-b)+12c212a(a+b)=12b(a-b)+12c2,化簡后,可得到勾股定理.
【知識運用】
如圖2,河道上A,B兩點(看作直線上的兩點)相距200米,C,D為兩個菜園(看作兩個點),AD⊥AB,BC⊥AB,垂足分別為A,B,AD=80米,BC=70米,現在菜農要在AB上確定一個抽水點P,使得抽水點P到兩個菜園C,D的距離和最短,則該最短距離為 250250米.
【知識遷移】
借助上面的思考過程,請直接寫出當0<x<15時,代數式x2+9+(15-x)2+25的最小值= 1717.
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
x
2
+
9
+
(
15
-
x
)
2
+
25
【考點】四邊形綜合題.
【答案】a(a+b);b(a-b);c2;a(a+b)=b(a-b)+c2;250;17
1
2
1
2
1
2
1
2
1
2
1
2
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/8/15 1:0:1組卷:510引用:6難度:0.1
相似題
-
1.閱讀下列材料:如圖(1),在四邊形ABCD中,若AB=AD,BC=CD,則把這樣的四邊形稱之為箏形.
(1)寫出箏形的兩個性質(定義除外).
①;②.
(2)如圖(2),在平行四邊形ABCD中,點E、F分別在BC、CD上,且AE=AF,∠AEC=∠AFC.求證:四邊形AECF是箏形.
(3)如圖(3),在箏形ABCD中,AB=AD=26,BC=DC=25,AC=17,求箏形ABCD的面積.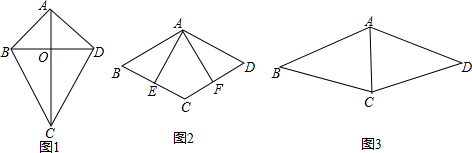 發布:2025/6/15 18:30:1組卷:1000引用:12難度:0.1
發布:2025/6/15 18:30:1組卷:1000引用:12難度:0.1 -
2.(1)如圖1,點P是?ABCD內的一點,分別過點B、C、D作AP的垂線BE、CF、DH,垂足分別為E、F、H,猜想BE、CF、DH三者之間的關系,并證明;
(2)如圖2,若點P在?ABCD的外部,△APB的面積為18,△APD的面積為3,求△APC的面積;
(3)如圖3,在(2)條件下,AB=BC,∠APC=∠ABC=90°,設AP、BP分別于CD相交于點M、N,=(請直接寫出結論).CPPM 發布:2025/6/15 11:0:2組卷:51引用:2難度:0.3
發布:2025/6/15 11:0:2組卷:51引用:2難度:0.3 -
3.已知矩形ABCD,把△BCD沿BD翻折,得△BDG,BG,AD所在的直線交于點E,過點D作DF∥BE交BC所在直線于點F.
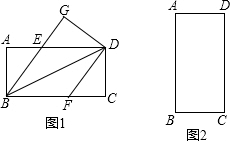
(1)如圖1,AB<AD,
①求證:四邊形BEDF是菱形;
②若AB=4,AD=8,求四邊形BEDF的面積;
(2)如圖2,若AB=8,AD=4,請按要求畫出圖形,并直接寫出四邊形BEDF的面積.發布:2025/6/15 10:30:2組卷:163引用:2難度:0.3


