綜合與實踐：【積累經驗】
我們在第十三章《全等三角形》中學習了全等三角形的性質和判定，在一些探究題中經常用以上知識轉化角和邊，進而解決問題．例如：我們在解決：“如圖1，在△ABC中，∠ACB=90°，AC=BC，線段DE經過點C，且AD⊥DE于點D，BE⊥DE于點E．
求證：AD=CE，CD=BE這個問題時，只要證明△ADC≌△CEB即可得到解決．
（1）請寫出證明過程：
【類比應用】
（2）如圖2，△ABC在平面直角坐標系中，∠ACB=90°，AC=BC，點A的坐標為（2，1），點C的坐標為（4，2），求點B的坐標．
【拓展提升】
（3）如圖3，在平面直角坐標系中，點A的坐標為（2，-1），點B的坐標為（5，0），以AB為一邊構造等腰直角三角形ABC，直接寫出在第一象限內滿足條件的所有點C的坐標 （1，2）或（4，3）或（3，1）（1，2）或（4，3）或（3，1）．
【考點】三角形綜合題．
【答案】（1，2）或（4，3）或（3，1）
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：390引用：4難度：0.2
相似題
-
1．如圖，在△ABC中，∠ACB=90°，CA=CB，∠MCN=45°，射線CM交直線AB于點P，過點A作AD⊥CM于點D，直線AD交直線CN于點E，連接BE．
（1）當點P在線段AB上時，如圖①，求證：AD+BE=DE；
（2）當點P在BA的延長線上時，如圖②；當點P在AB的延長線上時，如圖③，線段AD，DE，BE之間又有怎樣的數量關系？直接寫出你的猜想，不必證明．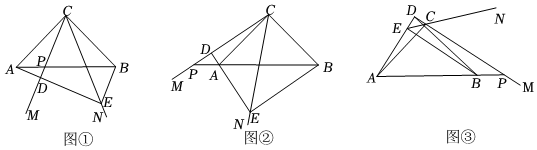
發布：2025/5/25 19:30:2組卷：79引用：1難度：0.3 -
2．某興趣小組探索等腰三角形中線段比值問題，部分探索活動如下：
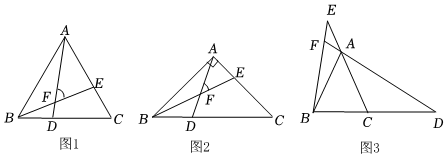
（1）如圖1，在△ABC中，AB=AC，∠ABC=60°，D，E分別是BC，AC邊上的點，∠AFE=∠ABC，則的值為 ．BEAD
（2）如圖2，在△ABC中，AB=AC，∠ABC=45°，D，E分別是BC，AC邊上的點，∠AFE=∠ABC，請你猜想的值，并給出證明；BEAD
（3）如圖3，在△ABC中，AB=AC，，D，E分別是BC，CA邊延長線上的點，∠DFB=∠ABC，請直接寫出cos∠ABC=512的值．BEAD發布：2025/5/26 0:0:1組卷：153引用：1難度：0.4 -
3．在△ABC中，AB=AC，BC=12，E為邊AC的中點，
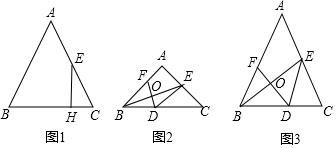
（1）如圖1，過點E作EH⊥BC，垂足為點H，求線段CH的長；
（2）作線段BE的垂直平分線分別交邊BC、BE、AB于點D、O、F．
①如圖2，當∠BAC=90°時，求BD的長；
②如圖3，設tan∠ACB=x,BD=y,求y與x之間的函數表達式和tan∠ACB的最大值．發布：2025/5/26 1:0:1組卷：278引用：2難度：0.1