問題發現：
（1）如圖①，正方形ABCD的邊長為2，對角線AC、BD相交于點O，E是AB上一點（點E不與A、B重合），將射線OE繞點O逆時針旋轉90°，所得射線與BC交于點F，則四邊形OEBF的面積為 11．
問題探究：
（2）如圖②，線段BQ=20，C為BQ上一點，在BQ上方作四邊形ABCD，使∠ABC=∠ADC=90°，且AD=CD，連接DQ，則DQ的最小值為 102102．
問題解讀：
（3）“綠水青山就是金山銀山”，某市在生態治理活動中新建了一處青山植物園，圖③為青山植物園花卉展示區的部分平面示意圖，在四邊形ABCD中，∠ABC=∠ADC=90°，AD=CD，AC=800米．其中AB、BD、BC為觀賞小路，設計人員考慮到為分散人流和便于觀賞，提出三條小路的長度和要取得最大，試求AB+BD+BC的最大值．
2
2
【考點】四邊形綜合題．
【答案】1；10
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：318引用：1難度：0.1
相似題
-
1．如圖，△ABC中，∠CAB與∠CBA均為銳角，分別以CA、CB為邊向△ABC外側作正方形CADE和正方形CBFG，再作DD1⊥直線AB于D1，FF1⊥直線AB于F1．
（1）如圖（1），過點C作CH⊥AB于H，求證：DD1+FF1=AB；
（2）如圖（2），連接EG，問△ABC的面積與△ECG的面積是否相等？請說明理由；
（3）如圖（3），過點C作CM⊥EG于M，延長MC交AB于點N，求證：AN=BN．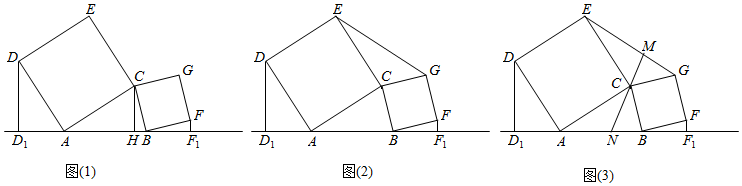
發布：2025/6/21 3:30:1組卷：127引用：3難度：0.5 -
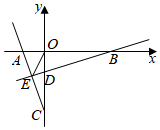2．在平面直角坐標系中，已知點A（a,0），C（0，b）且a,b滿足（a+1）2+=0．b+3
（1）直接寫出：a=，b=；
（2）點B在x軸正半軸上，過點B作BE⊥AC于點E，交y軸于點D（0，-1），連接OE，若OE平分∠AEB，求點B和點E的坐標；
（3）在（2）的條件下，若點P是直線BE上的動點，點Q是該平面內某一點，且以點P、Q、A、B為頂點的四邊形是菱形，直接寫出點P的坐標．發布：2025/6/21 13:30:2組卷：105引用：1難度：0.3 -
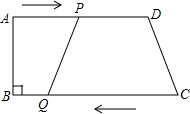3．如圖，在梯形ABCD中，AD∥BC，∠B=90°，AB=10cm,AD=20cm,BC=24cm,動點P從點A出發沿AD方向向點D以1cm/s的速度運動，動點Q從點C開始沿CB方向向點B以3cm/s的速度運動．P、Q兩點同時出發，設運動時間為t,當其中一點到達端點時，另一點隨之停止運動．
（1）當t=3時，PD=，CQ=．
（2）當t為何值時，四邊形CDPQ是平行四邊形？請說明理由．
（3）在運動過程中，設四邊形CDPQ的面積為S，寫出S與t的函數關系式，并求當t為何值時，S的值最大，最大值是多少？發布：2025/6/21 2:0:1組卷：147引用：2難度：0.3