綜合與實踐．
八年級同學在數學老師的指導下，以“三角形的旋轉”為主題，開展如下數學探究活動：
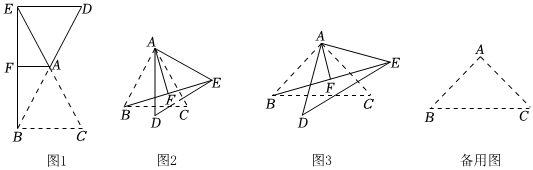
（1）如圖1，△ABC為等邊三角形，將△ABC繞點A旋轉180°，得到△ADE，連接BE，則∠EBC=9090°．若F是BE的中點，連接AF，則AF與DE的數量關系是 AF=12DFAF=12DF．
遷移探究：
（2）如圖2，（1）中的其他條件不變，當△ABC繞點A逆時針旋轉30°，得到△ADE，求出此時∠EBC的度數及AF與DE的數量關系．
拓展應用：
（3）如圖3，在Rt△ABC中，AB=AC=2，∠BAC=90°，將△ABC繞點A旋轉，得到△ADE，連接BE，F是BE的中點，連接AF．在旋轉過程中，當∠EBC=15°時，求AF的長．
1
2
1
2
【考點】幾何變換綜合題．
【答案】90；AF=DF
1
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/4 23:30:1組卷：595引用：2難度：0.2
相似題
-
1．【問題背景】
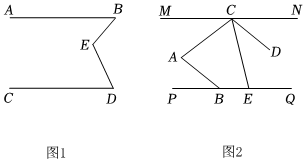
（1）如圖1，AB∥CD，E為AB，CD之間一點，連接BE，DE，得到∠BED，當∠CDE=65°，∠ABE=50°時，∠BED=度；
【類比探究】
（2）如圖1，AB∥CD，E為AB，CD之間一點，連接BE，DE，得到∠BED．試探究∠BED與∠B、∠D之間的數量關系，并說明理由；
【拓展延伸】
（3）如圖2，已知MN∥PQ，CD∥AB，點E在PQ上，∠ECN=∠CAB，請證明：∠ABP+∠DCE=∠CAB．
?發布：2025/6/6 9:0:1組卷：141引用：1難度：0.2 -
2．如圖①，邊長分別為a和b（a＞b）的兩個等邊三角形紙片△ABC和△ECD，連接BE，AD．
（1）若點B、C、D在同一直線上，如圖①，請直接寫出線段BE與AD之間的數量關系，．
（2）操作：△ABC不動，將△EDC繞點C逆時針方向旋轉任意角度α，如圖②，（1）中的結論是否還成立，若成立，僅就圖②的情形證明你的結論；若不成立，請說明理由．
（3）根據（2）的操作過程，若0°≤α≤360°，請你猜想當α為多少度時，線段BE的長度最大，最大長度是多少？當α為多少度時，線段BE的長度最小，最小長度是多少？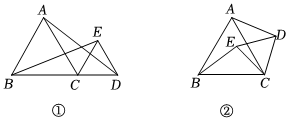
發布：2025/6/6 6:30:1組卷：74引用：1難度：0.4 -
3．如圖甲所示，已知點E在直線AB上，點F，G在直線CD上，且∠GEF=∠EFG，EF平分∠AEG．
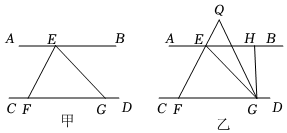
（1）判斷直線AB與直線CD是否平行，并說明理由．
（2）如圖乙所示，H是AB上點E右側一動點，∠EGH的平分線GQ交FE的延長線于點Q，①若∠HEG=90°，∠QGE=20°，
求∠Q的值．
②設∠Q=α，∠EHG=β．點H在運動過程中，寫出α和β的數量關系并說明理由．發布：2025/6/6 12:0:1組卷：110引用：1難度：0.2