【閱讀理解】
我們經常過某個點作已知直線的平行線，以便利用平行線的性質來解決問題．
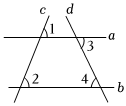
例如：如圖1，AB∥CD，點E、F分別在直線AB、CD上，點P在直線AB、CD之間，設∠AEP=∠α，∠CFP=∠β，求證：∠P=∠α+∠β．
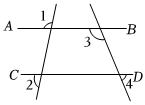
證明：如圖2，過點P作PQ∥AB，
∴∠EPQ=∠AEP=∠α，
∵PQ∥AB，AB∥CD，
∴PQ∥CD，
∴∠FPQ=∠CFP=∠β，
∴∠EPF=∠EPQ+∠FPQ=∠α+∠β．
即∠P=∠α+∠β．
可以運用以上結論解答下列問題：
【類比應用】
（1）如圖3，已知AB∥CD，已知∠D=40°，∠GAB=60°，求∠P的度數；
（2）如圖4，已知AB∥CD，點E在直線CD上，點P在直線AB上方，連接PA、PE．設∠A=∠α、∠CEP=∠β，則∠α、∠β、∠P之間有何數量關系？請說明理由；
【拓展應用】
（3）如圖5，已知AB∥CD，點E在直線CD上，點P在直線AB上方，連接PA、PE，∠PED的角平分線與∠PAB的角平分線所在直線交于點Q，求

1

2

∠

P

+

∠

Q

的度數．