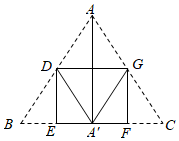
如圖，三角形紙片ABC，分別取AB、AC的中點D、G，沿DG折疊，使點A的對應點A′落在BC邊上；繼續將紙片折疊，使BD與DA′重合，CG與GA′重合，折痕分別為DE，GF，折疊后的三個三角形拼合形成一個矩形．連接AA′，則AA′為△ABC的高線．
（1）若△ABC面積為10，則矩形DEFG的面積為 55；
（2）若點A′恰好是邊BC的中點，求證：四邊形ADA′G為菱形；
（3）當△ABC滿足什么條件時，矩形DEFG為正方形，請說明理由．
【答案】5
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：83引用：3難度：0.7
相似題
-
1．如圖，等腰△ABC中，CA=CB=4，∠ACB=120°，點D在線段AB上運動（不與A、B重合），將△CAD與△CBD分別沿直線CA、CB翻折得到△CAP與△CBQ，給出下列結論：
①CD=CP=CQ；
②△PCQ面積的最小值為；435
③當點D在AB的中點時，△PDQ是等邊三角形；
④當PQ⊥BQ時，AD的長為；433
其中所有正確結論的序號是（ ）發布：2025/5/24 17:30:1組卷：96引用：3難度：0.6 -
2．如圖，直線y=-x+3交x軸于點A，交y軸于點B，點C是y軸的負半軸上的點，點C、D關于直線AB對稱，連接CD，交AB于點E，交x軸于點F，連接AD、BD，雙曲線33（x＞0）恰好經過點D．若∠BAD=45°，則k的值為（ ）y=kx發布：2025/5/24 19:30:1組卷：105引用：3難度：0.4 -
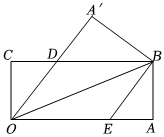3．如圖，在矩形OABC中，OA=8，AB=4．將△OAB沿OB所在直線翻折，點A落在點A′處，OA'與BC邊交于點D，過點B作BE∥OA′交OA于點E．
（1）求證：四邊形OEBD是菱形．
（2）求線段OD的長．發布：2025/5/24 18:0:1組卷：88引用：3難度：0.5