【問題提出】|a-1|+|a-2|+|a-3|+…+|a-2021|的最小值是多少?
【閱讀理解】
為了解決這個問題,我們先從最簡單的情況入手.|a|的幾何意義是a這個數在數軸上對應的點到原點的距離,那么|a-1|可以看作a這個數在數軸上對應的點到1的距離;|a-1|+|a-2|就可以看作a這個數在數軸上對應的點到1和2兩個點的距離之和.下面我們結合數軸研究|a-1|+|a-2|的最小值.
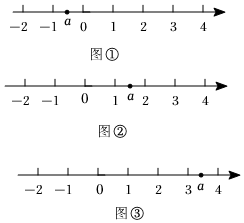
我們先看a表示的點可能的3種情況,如圖所示:
(1)如圖①,a在1的左邊,從圖中很明顯可以看出a到1和2的距離之和大于1.
(2)如圖②,a在1和2之間(包括在1,2上),可以看出a到1和2的距離之和等于1.
(3)如圖③,a在2的右邊,從圖中很明顯可以看出a到1和2的距離之和大于1.
所以a到1和2的距離之和最小值是1.
【問題解決】
(1)|a-3|+|a-6|的幾何意義是 a這個數在數軸上對應的點到表示3和6兩個數的點的距離之和a這個數在數軸上對應的點到表示3和6兩個數的點的距離之和;請你結合數軸探究:|a-3|+|a-6|的最小值是 33;
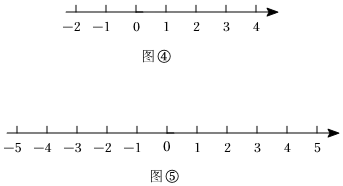
(2)請你結合圖④探究:|a-1|+|a-2|+|a-3|的最小值是 22,此時a為 22;
(3)|a-1|+|a-2|+|a-3|+|a-4|+|a-5|+|a-6|的最小值為 99;
(4)|a-1|+|a-2|+|a-3|+…|a-2021|的最小值為 10211101021110.
【拓展應用】
如圖⑤,已知a到-1,2的距離之和小于4,請寫出a的范圍為 -1.5<a<2.5-1.5<a<2.5.
【答案】a這個數在數軸上對應的點到表示3和6兩個數的點的距離之和;3;2;2;9;1021110;-1.5<a<2.5
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:541引用:2難度:0.4
相似題
-
 1.如圖,在不完整的數軸上有A,B兩點,它們所表示的兩個有理數絕對值相同,則關于原點位置描述正確的是( )
1.如圖,在不完整的數軸上有A,B兩點,它們所表示的兩個有理數絕對值相同,則關于原點位置描述正確的是( )A.在點A的左側 B.與點A或點B重合 C.在點B的右側 D.與線段AB的中點重合 發布:2025/5/24 17:30:1組卷:24引用:2難度:0.7 -
 2.如圖,將數軸上-4與8兩點間的線段六等分,五個等分點所對應的數依次為a1,a2,a3,a4,a5,則下列結論不正確的是( )
2.如圖,將數軸上-4與8兩點間的線段六等分,五個等分點所對應的數依次為a1,a2,a3,a4,a5,則下列結論不正確的是( )A.a3>0 B.|a1|=|a3| C.a1+a4>0 D.a1+a2+a3+a4+a5=0 發布:2025/5/24 18:0:1組卷:357引用:4難度:0.7 -
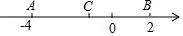 3.如圖,數軸上A、B兩點所表示的數分別是-4和2,點C是線段AB的中點,則點C所表示的數是.發布:2025/5/24 16:30:1組卷:5074引用:35難度:0.8
3.如圖,數軸上A、B兩點所表示的數分別是-4和2,點C是線段AB的中點,則點C所表示的數是.發布:2025/5/24 16:30:1組卷:5074引用:35難度:0.8


