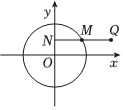
如圖，已知點M在圓O：x2+y2=4上運動，MN⊥y軸（垂足為N），點Q在NM的延長線上，且|QN|=2|MN|．
（1）求動點Q的軌跡方程；
（2）直線l：y=12x+m與（1）中動點Q的軌跡交于兩個不同的點A和B，圓O上存在兩點C、D，滿足|CA|=|CB|，|DA|=|DB|，求m的取值范圍．
y
=
1
2
x
+
m
【答案】（1）；
（2）．
x
2
16
+
y
2
4
=
1
（2）
-
2
2
＜
m
＜
2
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/10/2 2:0:1組卷：232引用：3難度：0.3