2023-2024學年寧夏寧夏育才中學高二（上）期中數學試卷

一．單項選擇題（每道小題只有一個正確答案，共8道小題，每小題5分，共計40分）

• 1．直線

  x

  +

  3

  y

  -

  1

  =

  0

  的傾斜角為（　　）

  A．30°

  B．60°

  C．120°

  D．150°
  組卷：218引用：6難度：0.7

  解析

• 2．已知向量

  a

  =（-1，2，1），

  b

  =（3，x,y），且

  a

  ∥

  b

  ，那么|

  b

  |=（　　）

  A． 3 6

  B．6

  C．9

  D．18
  組卷：431引用：24難度：0.8

  解析

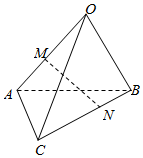• 3．如圖，空間四邊形OABC中，

  OA

  =

  a

  ，

  OB

  =

  b

  ，

  OC

  =

  c

  ，點M是OA的中點，點N在BC上，且

  CN

  =2

  NB

  ，設

  MN

  =x

  a

  +y

  b

  +z

  c

  ，則x,y,z的值為（　　）

  A． 1 2 ， 1 3 ， 2 3

  B． 1 2 ， 2 3 ， 1 3

  C．- 1 2 ， 2 3 ， 1 3

  D．- 1 2 ， 1 3 ， 2 3
  組卷：617引用：21難度：0.8

  解析

• 4．雙曲線

  x

  2

  a

  -

  y

  2

  2

  =

  1

  與橢圓

  x

  2

  4

  +

  y

  2

  a

  2

  =

  1

  的焦點相同，則a等于（　　）

  A．1

  B．-2

  C．1或-2

  D．2
  組卷：682引用：8難度：0.8

  解析

• 5．“1＜m＜3”是“方程

  x

  2

  3

  -

  m

  +

  y

  2

  m

  -

  1

  =

  1

  表示橢圓”的（　　）

  A．充要條件	B．充分不必要條件
  C．必要不充分條件	D．既不充分也不必要條件
  組卷：200引用：5難度：0.8

  解析

• 6．已知點A（-3，0）和點B（3，0），動點M滿足|MA|-|MB|=4，則點M的軌跡方程是（　　）

  A． x 2 4 - y 2 5 = 1 （ x ＜ 0 ）	B． x 2 4 - y 2 5 = 1 （ x ＞ 0 ）
  C． x 2 9 - y 2 5 = 1 （ x ＜ 0 ）	D． x 2 9 - y 2 5 = 1 （ x ＞ 0 ） ．
  組卷：136引用：3難度：0.9

  解析

• 7．若圓M：x²+y²-2x-2y-2=0上只有三個點到直線x+y+a=0的距離為1，求a的取值（　　）

  A． ± 2

  B． ± 2 2

  C． - 2 ± 2 2

  D． - 2 ± 2
  組卷：155引用：5難度：0.6

  解析

四．解答題（要求有詳細的解題步驟，共6道小題，共計70分）

• 21．在空間直角坐標系中，三棱錐P-ABC，

  AB

  =

  （

  2

  ，-

  1

  ，

  3

  ）

  ，

  AC

  =

  （

  -

  2

  ，

  1

  ，

  0

  ）

  ，

  AP

  =

  （

  3

  ，-

  1

  ，

  4

  ）

  ．
  （1）求三棱錐P-ABC的體積．
  （2）用求軌跡方程的思想方法，試求在空間直角坐標系中，以

  AB

  =

  （

  2

  ，-

  1

  ，

  3

  ）

  為方向向量，過點M（1，1，1）的直線方程．
  組卷：21引用：2難度：0.5

  解析

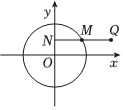• 22．如圖，已知點M在圓O：x²+y²=4上運動，MN⊥y軸（垂足為N），點Q在NM的延長線上，且|QN|=2|MN|．
  （1）求動點Q的軌跡方程；
  （2）直線l：

  y

  =

  1

  2

  x

  +

  m

  與（1）中動點Q的軌跡交于兩個不同的點A和B，圓O上存在兩點C、D，滿足|CA|=|CB|，|DA|=|DB|，求m的取值范圍．
  組卷：232引用：3難度：0.3

  解析