規定三角“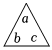
”表示abc,方框“
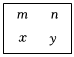”表示xm+yn．例如：
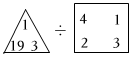=1×19×3÷（24+31）=3．請根據這個規定解答下列問題：
（1）計算：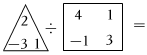
-32-32；
（2）代數式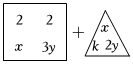
為完全平方式，則k=±3±3．
3
2
3
2
【答案】-；±3
3
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2025/6/2 1:0:1組卷：237引用：1難度：0.6