某水果店一種水果的日銷售量y（千克）與銷售價格x（元/千克）滿足一次函數(shù)關(guān)系，部分數(shù)據(jù)如表．
| 售價x（元/千克） | 6 | 8 | 10 |
| 日銷售量y（千克） | 20 | 18 | 16 |
（2）若將這種水果每千克的價格限定在6元～12元的范圍，求這種水果日銷售量的范圍；
（3）已知這種水果購進的價格為4元/千克，求這種水果在日銷售量不超過10千克的條件下可獲得的最大毛利潤．（假設：毛利潤=銷售額-購進成本）
【考點】二次函數(shù)的應用．
【答案】（1）這種水果日銷售量y與銷售價格x之間的函數(shù)關(guān)系式為y=-x+26；
（2）這種水果每千克的價格限定在6元～12元的范圍時，這種水果日銷售量的范圍為14千克～20千克；
（3）最大毛利潤為120元．
（2）這種水果每千克的價格限定在6元～12元的范圍時，這種水果日銷售量的范圍為14千克～20千克；
（3）最大毛利潤為120元．
【解答】
【點評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復制發(fā)布。
發(fā)布：2025/5/22 17:30:2組卷：140引用：2難度：0.5
相似題
-
1．某服裝店銷售某種衣服，其成本為每件60元，當售價為每件100元時，每月可銷售120件．由于疫情的影響，庫存積壓嚴重，為了減少庫存，該服裝店采取降價措施．據(jù)市場調(diào)查反映：銷售單價每降5元，則每月可多銷售20件．設每件的售價為x元（x為正整數(shù)），每月的銷售量為y件．
（1）直接寫出y與x的函數(shù)關(guān)系式；
（2）當銷售單件降低多少元時，每月獲得的利潤最大，最大利潤是多少？發(fā)布：2025/5/23 1:30:2組卷：27引用：1難度：0.5 -
2．某園藝公司計劃投資種植花卉及樹木，根據(jù)市場調(diào)查與預測，種植樹木的利潤y1（萬元）與投入資金x（萬元）成正比例關(guān)系，如圖1所示；種植花卉的利潤y2（萬元）與投入資金x（萬元）成二次函數(shù)關(guān)系，如圖2所示．
（1）分別求出利潤y1（萬元）與y2（萬元）關(guān)于投入資金x（萬元）的函數(shù)關(guān)系式；
（2）如果該園藝公司以8萬元資金投入種植花卉和樹木，他至少獲得多少利潤？他能獲取的最大利潤是多少？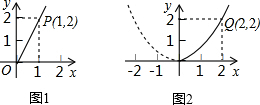
發(fā)布：2025/5/23 1:30:2組卷：149引用：5難度：0.7 -
3．某產(chǎn)品每件成本是10元，試銷階段每件產(chǎn)品的售價x（元）與日銷售量y（件）之間的關(guān)系如下表：
已知日銷售量y是售價x的一次函數(shù)．x（元） 15 20 30 … y（件） 25 20 10 …
（1）求y與x的函數(shù)表達式；
（2）當銷售價為多少時，每日的銷售利潤最大？最大利潤是多少？發(fā)布：2025/5/23 2:0:6組卷：157引用：3難度：0.6
相關(guān)試卷