當(dāng)前位置:
2023-2024學(xué)年黑龍江省哈爾濱市南崗區(qū)蕭紅中學(xué)九年級(jí)(上)月考數(shù)學(xué)試卷(9月份)(五四學(xué)制)>
試題詳情
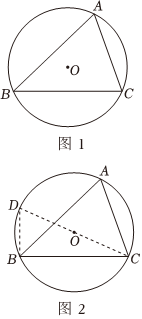
在學(xué)習(xí)了圓周角的定理及推論后,老師布置了這樣一個(gè)思考題“如圖1,△ABC內(nèi)接于⊙O,弦BC的長與∠A的正弦值的比值等于直徑.”同學(xué)們課下經(jīng)過探究、合作、交流,最后得到如下的解法:
|
證明:如圖2,連接CO并延長交⊙O于點(diǎn)D,連接BD. ∵CD是⊙O直徑, ∴ ∠DBC ∠DBC =90°.( 直徑所對(duì)的圓周角是直角 直徑所對(duì)的圓周角是直角 )∴ sin ∠ D = BC CD ? BC ? BC ∴∠D=∠A,( 同弧所對(duì)的圓周角相等 同弧所對(duì)的圓周角相等 )∴ sin ∠ A = sin ∠ D = BC CD ∴ BC sin A = BC BC CD = BC ? CD BC = CD |
(2)牛刀小試:如圖3,在⊙O中,弦AB=3,P為弧AB上一點(diǎn),∠P=135°,則⊙O的半徑為
3
2
2
3
2
2
(3)拓展延伸:如圖4,在⊙O中,弦AB=5,過點(diǎn)B作AB的垂線,在垂線上取一點(diǎn)C,過點(diǎn)C作AB的平行線交BC右側(cè)的圓于點(diǎn)D,若BC=4,CD=8,求⊙O的面積.
【考點(diǎn)】圓的綜合題.
【答案】∠DBC;直徑所對(duì)的圓周角是直角;同弧所對(duì)的圓周角相等;
3
2
2
【解答】
【點(diǎn)評(píng)】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/9/15 11:0:11組卷:99引用:2難度:0.4
相似題
-
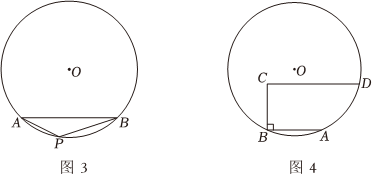
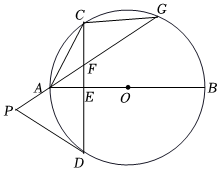 1.如圖,AB為⊙O的直徑,弦CD⊥AB于點(diǎn)E,F(xiàn)是CD上一點(diǎn),且AF=CF,點(diǎn)P在FA的延長線上,且∠PFD=∠PDF,延長PF與⊙O交于點(diǎn)G,連接AC,CG.
1.如圖,AB為⊙O的直徑,弦CD⊥AB于點(diǎn)E,F(xiàn)是CD上一點(diǎn),且AF=CF,點(diǎn)P在FA的延長線上,且∠PFD=∠PDF,延長PF與⊙O交于點(diǎn)G,連接AC,CG.
(1)求證:△AFC∽△ACG;
(2)求證:PD是⊙O的切線;
(3)若tanG=,BE-AE=34,求73的值.S△AFCS△CFG發(fā)布:2025/5/24 5:30:2組卷:72引用:1難度:0.4 -
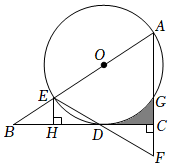 2.如圖,在△AEF中,∠F=∠AEF,以AE為直徑作⊙O,分別交邊AF和邊EF于點(diǎn)G和點(diǎn)D,過點(diǎn)D作DC⊥AF交AF于點(diǎn)C,延長CD交AE的延長線于點(diǎn)B,過點(diǎn)E作EH⊥BC于點(diǎn)H.
2.如圖,在△AEF中,∠F=∠AEF,以AE為直徑作⊙O,分別交邊AF和邊EF于點(diǎn)G和點(diǎn)D,過點(diǎn)D作DC⊥AF交AF于點(diǎn)C,延長CD交AE的延長線于點(diǎn)B,過點(diǎn)E作EH⊥BC于點(diǎn)H.
(1)試判斷BD與⊙O的位置關(guān)系,并說明理由;
(2)證明:EH=CF.
(3)若∠B=30°,AE=12,求圖中陰影部分的面積.發(fā)布:2025/5/24 6:0:2組卷:164引用:5難度:0.2 -
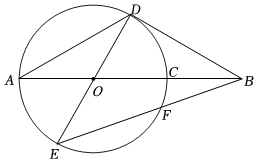 3.如圖,線段AB經(jīng)過⊙O的圓心O,交⊙O于A,C兩點(diǎn),AD為⊙O的弦,連接BD,∠A=∠ABD=30°,連接DO并延長,交⊙O于點(diǎn)E,連接BE交⊙O于點(diǎn)F.
3.如圖,線段AB經(jīng)過⊙O的圓心O,交⊙O于A,C兩點(diǎn),AD為⊙O的弦,連接BD,∠A=∠ABD=30°,連接DO并延長,交⊙O于點(diǎn)E,連接BE交⊙O于點(diǎn)F.
(1)求證:BD是⊙O的切線;
(2)求證:2AD2=DE?AB;
(3)若BC=1,求BF的長.發(fā)布:2025/5/24 6:30:2組卷:547引用:3難度:0.7


