閱讀材料.
我們知道,1+2+3+…+n=n(n+1)2,那么12+22+32+…+n2結(jié)果等于多少呢?
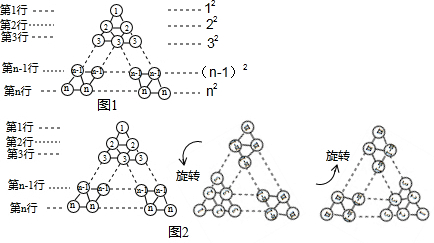
在圖1所示三角形數(shù)陣中,第1行圓圈中的數(shù)為1,即12,第2行兩個(gè)圓圈中數(shù)的和為2+2,即22,…;第n行n個(gè)圓圈中數(shù)的和為n+n+n+…+n,即n2.這樣,該三角形數(shù)陣中共有n(n+1)2個(gè)圓圈,所有圓圈中數(shù)的和為12+22+32+…+n2.
【規(guī)律探究】
將三角形數(shù)陣經(jīng)兩次旋轉(zhuǎn)可得如圖2所示的三角形數(shù)陣,觀察這三個(gè)三角形數(shù)陣各行同一位置圓圈中的數(shù)(如第n-1行的第一個(gè)圓圈中的數(shù)分別為n-1,2,n),發(fā)現(xiàn)每個(gè)位置上三個(gè)圓圈中數(shù)的和均為2n+12n+1,由此可得,這三個(gè)三角形數(shù)陣所有圓圈中數(shù)的總和為3(12+22+32+…+n2)=n(n+1)(2n+1)2n(n+1)(2n+1)2,因此,12+22+32+…+n2=n(n+1)(2n+1)6n(n+1)(2n+1)6.
【解決問題】
根據(jù)以上發(fā)現(xiàn),計(jì)算:12+22+32+…+1021+2+3+…+10的結(jié)果為77.
n
(
n
+
1
)
2
n
(
n
+
1
)
2
n
(
n
+
1
)
(
2
n
+
1
)
2
n
(
n
+
1
)
(
2
n
+
1
)
2
n
(
n
+
1
)
(
2
n
+
1
)
6
n
(
n
+
1
)
(
2
n
+
1
)
6
1
2
+
2
2
+
3
2
+
…
+
10
2
1
+
2
+
3
+
…
+
10
【考點(diǎn)】有理數(shù)的混合運(yùn)算;規(guī)律型:數(shù)字的變化類.
【答案】2n+1;;;7
n
(
n
+
1
)
(
2
n
+
1
)
2
n
(
n
+
1
)
(
2
n
+
1
)
6
【解答】
【點(diǎn)評(píng)】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/8/11 14:0:1組卷:272引用:4難度:0.7
相似題
-
1.計(jì)算下列各題(要求寫出解題關(guān)鍵步驟):
(1)3-2×(-5)2;
(2)-22-(-3)3×(-1)4-(-1)5;
(3);[(-32)3×(-43)2÷(-12)-32-(-3)3]×(-14)
(4).(-2)3×(-1)5-13÷[-(12)2]0.125×8+[1-32×(-2)]發(fā)布:2025/6/24 16:0:2組卷:120引用:4難度:0.5 -
2.某冷凍廠一個(gè)冷庫的室溫是2℃,現(xiàn)在一批食品需在-12℃冷藏,如果每小時(shí)降溫2℃,你知道幾個(gè)小時(shí)能降到所要求的溫度嗎?
發(fā)布:2025/6/24 17:0:1組卷:18引用:1難度:0.3 -
3.a※b是新規(guī)定的一種運(yùn)算法則:a※b=a2+2ab-1,若(-2)※3=x,則x=
.發(fā)布:2025/6/24 17:30:1組卷:46引用:3難度:0.9


