定義：我們知道，四邊形的一條對角線把這個四邊形分成了兩個三角形，如果這兩個三角形相似（不全等），我們就把這條對角線叫做這個四邊形的“相似對角線”．
理解：
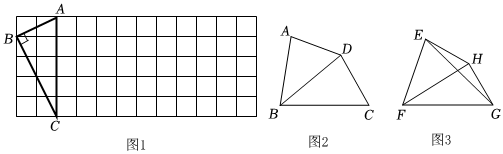
（1）如圖1，已知Rt△ABC在正方形網格中，請你在網格中找到一點D，使四邊形ABCD是以AC為“相似對角線”的四邊形（找出1個即可）；
（2）如圖2，在四邊形ABCD中，∠ABC=80°，∠ADC=140°，對角線BD平分∠ABC．
求證：BD是四邊形ABCD的“相似對角線”；
（3）如圖3，已知FH是四邊形EFCH的“相似對角線”，∠EFH=∠HFG=30°，連接EG，若△EFG的面積為43，求FH的長．
3
【考點】相似形綜合題．
【答案】（1）見解答；
（2）見解答；
（3）FH=4．
（2）見解答；
（3）FH=4．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：113引用：1難度：0.3
相似題
-
1．通過以前的學習，我們知道：“如圖1，在正方形ABCD中，CE⊥DF，則CE=DF”．
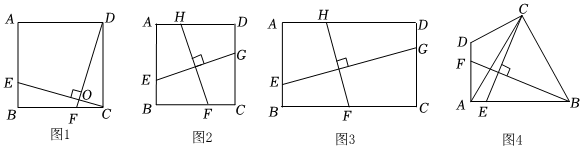
某數學興趣小組在完成了以上學習后，決定對該問題進一步探究：
（1）【問題探究】如圖2，在正方形ABCD中，點E，F，G，H分別在線段AB，BC，CD，DA上，且EG⊥FH，試猜想=；EGFH
（2）【知識遷移】如圖3，在矩形ABCD中，AB=m,BC=n,點E，F，G，H分別在線段AB，BC，CD，DA上，且EG⊥FH，試猜想的值，并證明你的猜想；EGFH
（3）【拓展應用】如圖4，在四邊形ABCD中，∠DAB=90°，∠ABC=60°，AB=BC，點E，F分別在線段AB，AD上，且CE⊥BF，求的值．CEBF發布：2025/5/21 13:30:2組卷：743引用：6難度：0.1 -
2．正方形ABCD中，AB=2，點E是對角線BD上的一動點，∠DAE=α（α≠45°）．將△ADE沿AE翻折得到△AFE，直線BF交射線DC于點G．
（1）當0°＜α＜45°時，求∠DBG的度數（用含α的式子表示）；
（2）點E在運動過程中，試探究的值是否發生變化？若不變，求出它的值．若變化，請說明理由；DGDE
（3）若BF=FG，求α的值．
發布：2025/5/21 14:0:2組卷：648引用：2難度：0.1 -
3．綜合與實踐課上，老師讓同學們以“矩形的折疊”為主題開展數學活動．
操作探究：
（1）如圖1，矩形紙片ABCD中，AD=2，，將矩形紙片ABCD對折，使點A與點D重合，點B與點C重合，再將矩形紙片ABCD展開，得到折痕MN，連接CM，折疊△DCM，點D的對應點為點D′，過D′作D′G⊥AD于點G，則D′G的長度為 ．AB=3
遷移探究：
小華將矩形紙片換成正方形紙片，繼續探究，過程如下：
操作一：如圖①，將正方形紙片ABCD對折，使點A與點D重合，點B與點C重合，再將正方形紙片ABCD展開，得到折痕MN；
操作二：如圖②，將正方形紙片ABCD的右上角沿MC折疊，得到點D的對應點D′；
操作三：如圖③，將正方形紙片ABCD的左上角沿MD'折疊再展開，折痕MD與邊AB交于點P．
問題解決：請在圖③中解決下列問題：
（2）求證：BP=D′P；
（3）求證：AP：BP=2：1．
拓展探究：
（4）在圖③的基礎上，將正方形紙片ABCD的左下角沿CD'折疊再展開，折痕CD'與邊AB交于點Q，如圖④．試探究：=（直接寫出結果，不需證明）．PQAB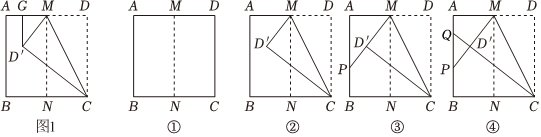
發布：2025/5/21 13:0:1組卷：153引用：1難度：0.4