問題提出:將正m邊形(m≥3)不斷向外擴展,每擴展一個正m邊形每條邊上的點的個數(shù)(以下簡稱“點數(shù)”)就增加一個,則n個正m邊形的點數(shù)總共有多少個?
問題探究:為了解決上面的問題,我們將采取將一般問題特殊化的策略,先從簡單和具體的情形入手:
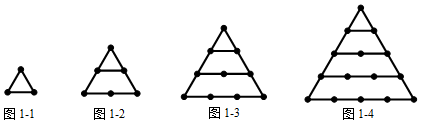
探究一:n個正三角形的點數(shù)總共有多少個?
如圖1-1,1個正三角形的點數(shù)總共有3個;如圖1-2,2個正三角形的點數(shù)總共有6個;如圖1-3,3個正三角形的點數(shù)總共有10個;…;n個正三角形的點數(shù)總共有 (n+1)(n+2)2(n+1)(n+2)2個.
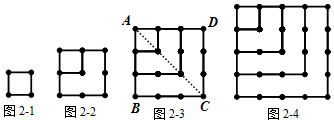
探究二:n個正四邊形的點數(shù)總共有多少個?
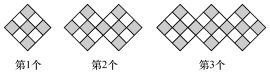
如圖2-1,1個正四邊形的點數(shù)總共有4個;如圖2-2,2個正四邊形的點數(shù)總共有9個;
如圖2-3,連接AC,得到兩個三角形△ABC和△ADC,這兩個三角形相同之處在于,BC邊與CD邊都有相同個數(shù)的點,即4個點,并且與BC、CD平行的邊上依次減少一個點直至頂點A,每個三角形都有10個點,兩個三角形就是2×10個點.因為這兩個三角形在AC上有4個點重合,所以3個正四邊形的點數(shù)總共有2×10-4=16(個).
如圖2-4,4個正四邊形的點數(shù)總共有 2525個;……n個正四邊形的點數(shù)總共有 (n+1)2(n+1)2個.
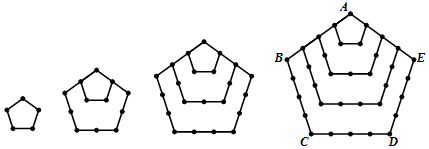
探究三:n個正五邊形的點數(shù)總共有多少個?
類比探究二的方法,求4個正五邊形的點數(shù)總共有多少個?并敘述你的探究過程.
n個正五邊形的點數(shù)總共有 12(n+1)(3n+2)12(n+1)(3n+2)個.
探究四:n個正六邊形的點數(shù)總共有 (n+1)(2n+1)(n+1)(2n+1)個.

問題解決:n個正m邊形的點數(shù)總共有 (n+1)[n(m-2)2+1](n+1)[n(m-2)2+1]個.
實際應(yīng)用:若99個正m邊形的點數(shù)總共有39700個,求m的值.
(
n
+
1
)
(
n
+
2
)
2
(
n
+
1
)
(
n
+
2
)
2
1
2
1
2
n
(
m
-
2
)
2
n
(
m
-
2
)
2
【答案】;25;(n+1)2;(n+1)(3n+2);(n+1)(2n+1);(n+1)[+1]
(
n
+
1
)
(
n
+
2
)
2
1
2
n
(
m
-
2
)
2
【解答】
【點評】
聲明:本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有,未經(jīng)書面同意,不得復(fù)制發(fā)布。
發(fā)布:2024/6/27 10:35:59組卷:331引用:3難度:0.3
相似題
-
1.如圖,將一條長度為1的線段三等分,然后取走其中的一份,稱為第一次操作;再將余下的每一條線段三等分,然后取走其中一份,稱為第二次操作;…如此重復(fù)操作,當(dāng)?shù)趎次操作結(jié)束時,被取走的所有線段長度之和為.
 發(fā)布:2025/5/25 21:0:1組卷:829引用:45難度:0.7
發(fā)布:2025/5/25 21:0:1組卷:829引用:45難度:0.7 -
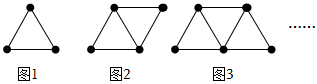
2.如圖是用火柴棍拼成一個由三角形組成的圖形,拼第一個圖形共需要3根火柴棍;拼第二個圖形共需要5根火柴棍;拼第三個圖形共需要7根火柴棍;…照這樣拼圖,則第4個圖形需要 根火柴棍,第n個圖形需要 根火柴棍.
 發(fā)布:2025/5/26 2:30:2組卷:161引用:4難度:0.7
發(fā)布:2025/5/26 2:30:2組卷:161引用:4難度:0.7 -
3.如圖是一組有規(guī)律的圖案,它們是由邊長相同的小正方形組成,其中部分小正方形涂有陰影,依此規(guī)律,第10個圖案中涂有陰影的小正方形的個數(shù)為( )
A.50 B.45 C.41 D.36 發(fā)布:2025/5/25 19:30:2組卷:652引用:4難度:0.6
相關(guān)試卷


