在我們蘇科版七下第九章的學習中，對同一個圖形的面積可以從不同的角度思考，用不同的式子表示．
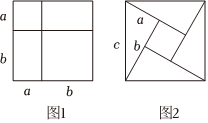
（1）用不同的方法計算圖1的面積可得到一個等式：（a+b）2=a2+2ab+b2（a+b）2=a2+2ab+b2．
（2）圖2是我國古代數學家趙爽的“勾股圓方圖”，它是由四個能完全重合的直角三角形與中間的一個小正方形拼成的一個大正方形，設直角三角形的較短直角邊為a,較長直角邊為b,最長的斜邊為c.
①探究a2、b2、c2之間的數量關系（按給出的格式完成探究）．
∵S（大正方形）=c2c2，（整體角度填寫）
S（大正方形）=4×12ab+（b-a）24×12ab+（b-a）2（局部組合角度填寫）=a2+b2a2+b2，（化簡結果）
∴a2+b2a2+b2=c2c2．
②根據①中的探究，請用文字語言總結出直角三角形的三邊具有的性質．
③在直角△ABC中，∠C=90°，邊長a、b、c滿足a+b=14，c=10，求△ABC的面積．
4
×
1
2
ab
+
（
b
-
a
）
2
4
×
1
2
ab
+
（
b
-
a
）
2
【考點】四邊形綜合題．
【答案】（a+b）2=a2+2ab+b2；c2；；a2+b2；a2+b2；c2
4
×
1
2
ab
+
（
b
-
a
）
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/11 8:0:9組卷：137引用：3難度：0.3
相似題
-
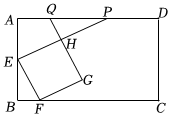1．如圖，在矩形ABCD中，點E為AB的中點，點F在BC邊上，以EF為邊，在矩形ABCD的內部作正方形EFGH，延長EH交AD邊于點P，延長GH交AD邊于點Q．
（1）若點H為EP的中點，
①求證：BE=2BF；
②若，△HQP和△AEP的周長分別為m,n,求EF=5的值；mn
（2）若S△AEP=9S△BEF，求的值．S△AEPS△HQP發布：2025/5/30 12:30:2組卷：125引用：1難度：0.3 -
2．小星和小紅在學習了正方形的相關知識后，對正方形內一些特殊線段的關系進行探究．
（1）問題解決
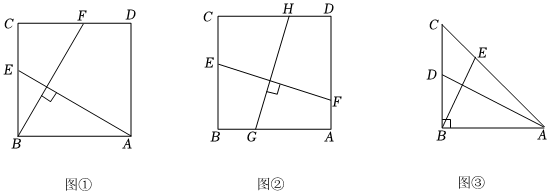
如圖①，在正方形ABCD中，E，F分別是BC，CD邊上的點，連接AE，BF，且AE⊥BF，求證：△ABE≌△BCF；
（2）類比探究
如圖②，在正方形ABCD中，E，F，G，H分別是BC，AD，AB，CD邊上的點，連接EF，GH，且EF⊥GH，求證：EF=GH；
（3）遷移應用
如圖③，在Rt△ABC中，∠ABC=90°，AB=BC，D是BC的中點，E是AC邊上的點，連接AD，BE，且BE⊥AD，求的值．AECE發布：2025/5/30 12:0:2組卷：250引用：3難度：0.1 -
3．如圖①，在四邊形ABCD中，AD=BC，P是對角線BD的中點，M是DC的中點，N是AB的中點．
（1）求證：∠PMN=∠PNM．
【結論應用】
（2）如圖②，在上邊題目的條件下，延長圖中的線段AD交NM的延長線于點E，延長線段BC交NM的延長線于點F．求證：∠AEN=∠F．
（3）若（1）中的∠A+∠ABC=122°，則∠F的大小為 ．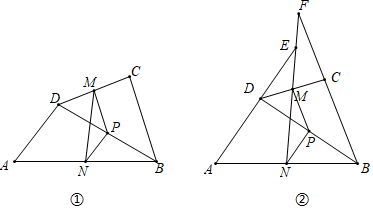
發布：2025/5/30 12:0:2組卷：194引用：7難度：0.4