甲乙兩地分別對本地各40萬人接種某種疫苗，甲地在前期完成5萬人接種后，甲、乙兩地同時以相同速度接種，甲地經(jīng)過a天后接種人數(shù)達(dá)到25萬人，由于情況變化，接種速度放緩，結(jié)果100天完成接種任務(wù)，乙地80天完成接種任務(wù)，在某段時間內(nèi)，甲、乙兩地的接種人數(shù)y（萬人）與各自接種時間x（天）之間的關(guān)系如圖所示．
（1）乙地每天接種 0.50.5萬人，a=4040；
（2）當(dāng)甲地接種速度放緩后，求y關(guān)于x的函數(shù)表達(dá)式；
（3）當(dāng)乙地完成接種任務(wù)時，求甲地未接種疫苗的人數(shù)．
【考點(diǎn)】一次函數(shù)的應(yīng)用．
【答案】0.5；40
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/9/26 6:0:3組卷：458引用：4難度：0.5
相似題
-
1．我市通過“互聯(lián)網(wǎng)+”“大數(shù)據(jù)”等新科技，打造“智慧停車平臺”，著力化解城市“停車難”問題．市內(nèi)某智慧公共停車場的收費(fèi)標(biāo)準(zhǔn)是停車不超過30分鐘，不收費(fèi)；超過30分鐘，不超過60分鐘，計1小時，收費(fèi)3元；超過1小時后，超過1小時的部分按每小時2元收費(fèi)（不足1小時，按1小時計）．
（1）若張先生某次在該停車場停車2小時10分鐘，應(yīng)交停車費(fèi) 元；若李先生也在該停車場停車，并支付了11元停車費(fèi)，則該停車場是按 小時（填整數(shù)）計時收費(fèi)．
（2）當(dāng)x取整數(shù)且x≥1時，求該停車場停車費(fèi)y（元）關(guān)于停車計時x（小時）的函數(shù)解析式．發(fā)布：2025/5/23 1:30:2組卷：155引用：2難度：0.7 -
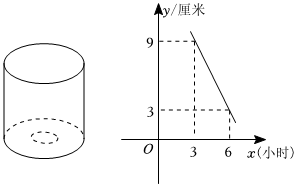2．如圖，“漏壺”是一種古代計時器，在它內(nèi)部盛一定量的水，水從壺下的小孔漏出，壺內(nèi)壁有刻度，人們根據(jù)壺中水面的位置計算時間．用x（小時）表示漏水時間，y（厘米）表示壺底到水面的高度．根據(jù)記時過程中記錄到的部分?jǐn)?shù)據(jù)繪制出y與x的函數(shù)圖象，則剛開始時，壺底到水面的高度為（ ）發(fā)布：2025/5/23 2:0:6組卷：221引用：1難度：0.7 -
3．一個深為6米的水池積存著少量水，現(xiàn)在打開水閥進(jìn)水，下表記錄了2小時內(nèi)5個時刻的水位高度，其中x表示進(jìn)水用時（單位：小時），y表示水位高度（單位：米）．
為了描述水池水位高度與進(jìn)水用時的關(guān)系，現(xiàn)有以下三種函數(shù)模型供選擇：y=kx+b（k≠0），y=ax2+bx+c（a≠0），y=x 0 0.5 1 1.5 2 y 1 1.5 2 2.5 3 （k≠0）．kx
（1）在平面直角坐標(biāo)系中描出表中數(shù)據(jù)對應(yīng)的點(diǎn)，再選出最符合實(shí)際的函數(shù)模型，求出相應(yīng)的函數(shù)表達(dá)式，并畫出這個函數(shù)的圖象．
（2）當(dāng)水位高度達(dá)到5米時，求進(jìn)水用時x.發(fā)布：2025/5/22 23:30:1組卷：1077引用：6難度：0.5