在一次數學活動課上，老師要求同學們畫15°、30°和60°角，小強同學身旁沒有量角器，也沒有圓規、三角尺，他靈機一動，想到了折紙的辦法：他拿出一張矩形紙片ABCD，先對折使AD與BC重合，如圖一，得到折痕EF，把紙片展開，再一次折疊紙片ABCD，使點A落在EF上的N處，并使折痕經過點B，得到折痕BM和線段BN．
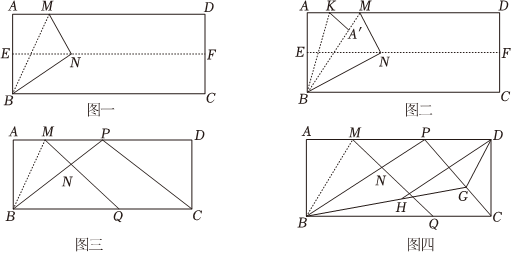
（1）請直接寫出∠ABM的度數，并說明理由；
（2）在圖一的線段AM上取一點K，將△ABK沿著直線BK折疊，如圖二，使得A點恰好落在線段BM上，求tan∠ABK；
（3）若M為AD邊上的一點，如圖三，將△ABM沿直線BM折疊，A的對應點為N，延長MN交BC邊于點Q，延長BN交AD邊于點P，連接CP．
①若ADAB=n，當AB=2cm時，若存在唯一的點P，使得四邊形MQCP為平行四邊形，求n的值；
②在①的條件下，若G為線段CP上一動點，如圖四，連接BG，取線段BG的中點H，連接DH，求DH的最小值．
AD
AB
=
n
【考點】解三角形．
【答案】（1）∠ABM=30°；（2）；（3）①n=2；②．
tan
∠
ABK
=
2
-
3
DH
=
2
2
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/7/29 8:0:9組卷：133引用：4難度：0.1
相似題
-
1．在①
，②2a-c=2bcosC，③（a-b）（a+b）=（a-c）c這三個條件中任選一個，補充在下面的問題中，并解答該問題．3（a-bcosC）=csinB
在△ABC中，內角A，B，C的對邊分別是a,b,c,且滿足 _____，．b=23
（1）若a+c=4，求△ABC的面積；
（2）求△ABC周長l的取值范圍．發布：2024/12/29 13:0:1組卷：287引用：4難度：0.5 -
2．已知燈塔A在海洋觀察站C的北偏東65°，距離海洋觀察站C的距離為akm,燈塔B在海洋觀察站C的南偏東55°，距離海洋觀察站C的距離為3akm,則燈塔A與燈塔B的距離為（ ）
發布：2024/12/30 4:0:3組卷：50引用：3難度：0.7 -
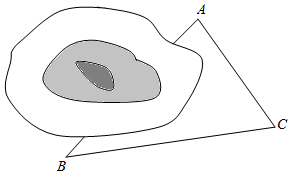3．如圖，在鐵路建設中，需要確定隧道兩端的距離（單位：百米），已測得隧道兩端點A，B到某一點C的距離分別為5和8，∠ACB=60°，則A，B之間的距離為（ ）發布：2024/12/29 13:0:1組卷：295引用：5難度：0.7