在正方形ABCD中，點(diǎn)E是對(duì)角線AC上的一點(diǎn)，且AE=1nAC（n＞2），將線段AE繞著點(diǎn)E順時(shí)針旋轉(zhuǎn)至EF，記旋轉(zhuǎn)角為α（0＜α≤180°），連接AF、CF，并以CF為斜邊在其上方作△CFG∽△CAD，連接DG．
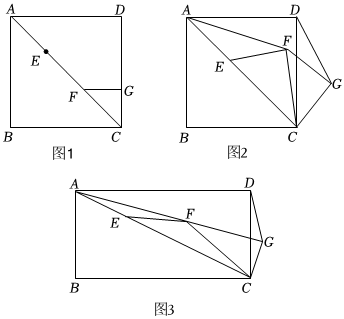
（1）特例探究：如圖1，當(dāng)n=3，α=180°時(shí)，線段AF與DG的數(shù)量關(guān)系為 AF=2DGAF=2DG；
（2）問(wèn)題探究：如圖2所示，在旋轉(zhuǎn)的過(guò)程中，
①（1）中的結(jié)論是否依然成立，若成立，請(qǐng)說(shuō)明理由；
②當(dāng)n=83，∠EFC=90° 時(shí)，若AB=42，求DG的長(zhǎng)度；
（3）拓展提升：若正方形ABCD改為矩形ABCD，且ABAD=12，其它條件不變，在旋轉(zhuǎn)的過(guò)程中，當(dāng)A、F、G三點(diǎn)共線時(shí)，如圖3所示，若n=4，CG=m,直接寫(xiě)出DG的長(zhǎng)度．（用含m的式子表示）
AE
=
1
n
AC
（
n
＞
2
）
2
2
n
=
8
3
AB
=
4
2
AB
AD
=
1
2
【考點(diǎn)】相似形綜合題．
【答案】AF=DG
2
【解答】
【點(diǎn)評(píng)】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書(shū)面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/5/27 14:0:0組卷：972引用：2難度：0.3
相似題
-
1．如圖1，在Rt△ABC中，∠BAC=90°，D為邊AB上一點(diǎn)，∠ACD=∠B．
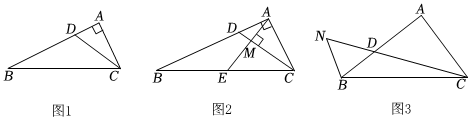
（1）求證：AC2=AD?AB；
（2）如圖2，過(guò)點(diǎn)A作AM⊥CD于M，交BC于點(diǎn)E，若AB=4AD，求的值；AMME
（3）如圖，N為CD延長(zhǎng)線上一點(diǎn)，連接BN，且∠NBD=2∠ACD，若，直接寫(xiě)出tan∠ACD=1n（n＞1）的值（用含n的代數(shù)式表示）．NDDC發(fā)布：2025/5/22 10:30:1組卷：557引用：4難度：0.1 -
2．如圖，在Rt△ABC中，∠ACB=90°，AC=6，BC=3．點(diǎn)D是邊AC上一動(dòng)點(diǎn)（不與A、C重合），聯(lián)結(jié)BD，過(guò)點(diǎn)C作CF⊥BD，分別交BD、AB于點(diǎn)E、F．
（1）當(dāng)CD=2時(shí)，求∠ACF的正切值；
（2）設(shè)CD=x,，求y關(guān)于x的函數(shù)解析式，并寫(xiě)出x的定義域；AFBF=y
（3）聯(lián)結(jié)FD并延長(zhǎng)，與邊BC的延長(zhǎng)線相交于點(diǎn)G，若△DGC與△BAC相似，求的值．AFBF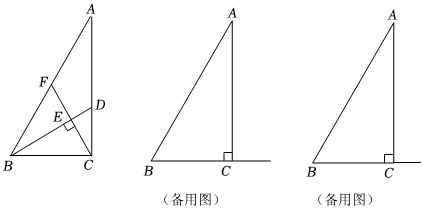
發(fā)布：2025/5/22 11:30:2組卷：530引用：1難度：0.4 -
3．【問(wèn)題提出】
在一次折紙活動(dòng)課上，老師提出這樣一個(gè)問(wèn)題：如何把一張正方形的紙通過(guò)折疊的方式等分成若干份？
【解決問(wèn)題】
以下是某個(gè)小組的活動(dòng)過(guò)程：若是等分成兩份，如圖①直接對(duì)折，四等分、八等分在二等分的基礎(chǔ)上進(jìn)行對(duì)折即可，那三等分呢？
學(xué)習(xí)過(guò)相似三角形的相關(guān)知識(shí)后，小明提出了如下方法：如圖②，折出AD、BC的中點(diǎn)E、F，連接AF、CE交對(duì)角線BD于點(diǎn)G、H，過(guò)點(diǎn)G、H折出AB、CD的平行線，折痕MN、PQ三等分正方形紙片．
（1）小明的想法正確嗎？若正確，請(qǐng)證明：
【類比學(xué)習(xí)】
（2）尺規(guī)作圖：如圖③，請(qǐng)你用尺規(guī)作圖，作線段AB的三等分點(diǎn)．（保留作圖痕跡，并簡(jiǎn)要說(shuō)明作法）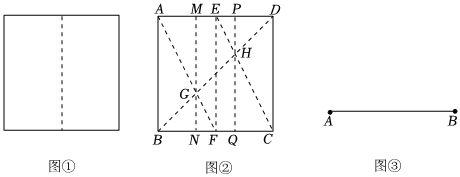
發(fā)布：2025/5/22 14:0:1組卷：248引用：3難度：0.4
相關(guān)試卷