為充分了解廣大業主對小區物業服務的滿意程度及需求，進一步提升物業服務質量，現對小區物業開展業主滿意度調查，從小區中選出100名業主，對安保服務和維修服務的評價進行統計，數據如表．
（1）完成下面的2×2列聯表，并根據小概率值α=0.001的獨立性檢驗判斷業主對安保服務的滿意度與對維修服務的滿意度是否有關聯；
| 評價 | 服務 | 合計 | |
| 安保服務 | 維修服務 | ||
| 滿意 | 57 | ||
| 不滿意 | 15 | ||
| 合計 | 40 | ||
附：①
χ
2
=
n
（
ad
-
bc
）
2
（
a
+
b
）
（
c
+
d
）
（
a
+
c
）
（
b
+
d
）
②臨界值表
| α | 0.1 | 0.05 | 0.01 | 0.005 | 0.001 |
| xα | 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
【考點】離散型隨機變量的均值（數學期望）．
【答案】（1）表格見解析，認為業主對安保服務的滿意度與對維修服務的滿意度有關聯；
（2）分布列見解析，E（X）=1．
（2）分布列見解析，E（X）=1．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/7 8:0:9組卷：29引用：3難度：0.5
相似題
-
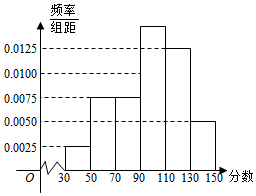1．某市舉行“中學生詩詞大賽”，分初賽和復賽兩個階段進行，規定：初賽成績大于90分的具有復賽資格，某校有800名學生參加了初賽，所有學生的成績均在區間（30，150]內，其頻率分布直方圖如圖．
（Ⅰ）求獲得復賽資格的人數；
（Ⅱ）從初賽得分在區間（110，150]的參賽者中，利用分層抽樣的方法隨機抽取7人參加學校座談交流，那么從得分在區間（110，130]與（130，150]各抽取多少人？
（Ⅲ）從（Ⅱ）抽取的7人中，選出3人參加全市座談交流，設X表示得分在區間（130，150]中參加全市座談交流的人數，求X的分布列及數學期望E（X）．發布：2024/12/29 13:30:1組卷：134引用：7難度：0.5 -
2．設離散型隨機變量X的分布列如表：
若離散型隨機變量Y=-3X+1，且E（X）=3，則（ ）X 1 2 3 4 5 P m 0.1 0.2 n 0.3 發布：2024/12/29 13:0:1組卷：200引用：6難度：0.5 -
3．從4名男生和2名女生中任選3人參加演講比賽，用X表示所選3人中女生的人數，則E（X）為（ ）
發布：2024/12/29 13:30:1組卷：139引用：6難度：0.7