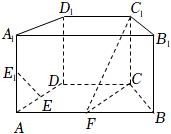
如圖，在直四棱柱ABCD-A₁B₁C₁D₁中，底面ABCD為等腰梯形，AB∥CD，AB=4，BC=CD=2，AA₁=2，E，E₁分別是棱AD，AA₁的中點．
（1）設F是棱AB的中點，證明：直線EE₁∥平面FCC₁；
（2）證明：平面D₁AC⊥平面BB₁C₁C．

【答案】見試題解答內容

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/4/20 14:35:0組卷：1847引用：15難度：0.5

相似題

1．已知平面α與平面β間的距離為3，定點A∈α，設集合S={B∈β|AB=5}，則S表示的曲線的長度為（　　）
A．6π B．8π C．10π D．12π
發布：2024/10/7 1:0:1組卷：49引用：3難度：0.7
解析
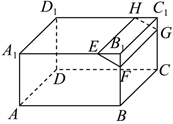2．如圖，在長方體ABCD-A₁B₁C₁D₁中，
A
1
E
E
B
1
=
BF
F
B
1
=
CG
G
C
1
=
D
1
H
H
C
1
=
2
，則下列說法錯誤的是（　　）
A．BD₁∥GH B．BD與EF異面
C．EH∥平面ABCD D．平面EFGH∥平面A₁BCD₁
發布：2024/11/30 13:0:1組卷：432引用：5難度：0.5
解析
3．如圖，正方體ABCD-A₁B₁C₁D₁中，M，N，E，F分別是棱A₁B₁，A₁D₁，B₁C₁，C₁D₁的中點．
（1）求證：直線MN∥平面EFDB；
（2）求證：平面AMN∥平面EFDB．
發布：2024/12/29 9:0:1組卷：187引用：3難度：0.3
解析

相關試卷

A．BD₁∥GH	B．BD與EF異面
C．EH∥平面ABCD	D．平面EFGH∥平面A₁BCD₁

如圖，在直四棱柱ABCD-A1B1C1D1中，底面ABCD為等腰梯形，AB∥CD，AB=4，BC=CD=2，AA1=2，E，E1分別是棱AD，AA1的中點．（1）設F是棱AB的中點，證明：直線EE1∥平面FCC1；（2）證明：平面D1AC⊥平面BB1C1C．