綜合與實踐：
問題情境
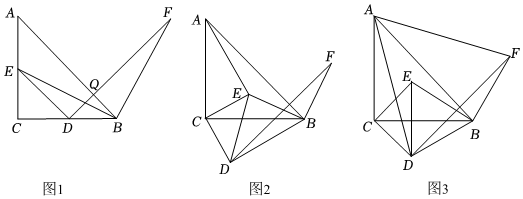
圖形變換包括平移、旋轉、對稱、位似等，其中旋轉就是將圖形上的每一點在平面內繞著旋轉中心旋轉固定角度的位置移動，其中“旋”是過程，“轉”是結果．旋轉的性質則是解決實際問題的關鍵．數學活動課上，老師讓同學們根據如下問題情境，發現并提出問題．如圖1，△ABC與△EDC都是等腰直角三角形，點E，D分別在AC和BC上，連接EB．將線段EB繞點B順時針旋轉90°，得到的對應線段為BF．連接BE，DF．“興趣小組”提出了如下兩個問題：
①AE=BD，AE⊥BD；②DF=AB，DF⊥AB
解決問題：
（1）請你證明“興趣小組”提出的第②個問題．
探索發現：
（2）“實踐小組”在圖1的基礎上，將△EDC繞點C順時針旋轉角度α（0°＜α＜90°），其它條件保持不變，得到圖2．
①請你幫助“實踐小組”探索：“興趣小組”提出的兩個問題是否還成立？如果成立，請給出證明；若不成立，請說明理由．
②如圖3，當AD=AF時，請求出此時旋轉角α的大小．
【考點】相似形綜合題．
【答案】（1）證明見解答；
（2）①都成立；
②45°．
（2）①都成立；
②45°．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：278引用：2難度：0.4
相似題
-
1．如果一個三角形的一個內角等于另一個內角的2倍，我們稱這樣的三角形為倍角三角形，并稱這兩個角的公共邊為底邊．
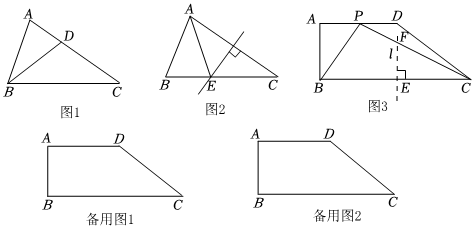
例如：若△ABC中，∠A=2∠B，則△ABC為以邊AB為底邊的倍角三角形．
（1）已知△ABC為倍角三角形，且∠ABC=2∠C．
①如圖1，若BD為△ABC的角平分線，則圖中相等的線段有 ，圖中相似三角形有 ；
②如圖2，若AC的中垂線交邊BC于點E，連接AE，則圖中等腰三角形有 ．
問題解決
（2）如圖3，現有一塊梯形板材ABCD，AD∥BC，∠A=90°，AB=48，BC=132，AD=68．工人師傅想用這塊板材裁出一個△BCP型部件，使得點P在梯形ABCD的邊上，且△BCP為以BC為底邊的倍角三角形．工人師傅在這塊板材上的作法如下：
①作BC的中垂線l交BC于點E；
②在BC上方的直線l上截取EF=33，連接CF并延長，交AD于點P；
③連接BP，得△BCP．
1）請問，若按上述作法，裁得的△BCP型部件是否符合要求？請證明你的想法．
2）是否存在其它滿足要求的△BCP？若存在，請畫出圖形并求出CP的長；若不存在，請說明理由．發布：2025/5/24 13:30:2組卷：255引用：4難度：0.1 -
2．在平行四邊形ABCD中，AD=8，DC=6，∠FED的頂點在BC上，EF交直線AB于F點．
（1）如圖1，若∠FED=∠B=90°，BE=5，求BF的長；
（2）如圖2，在AB上取點G，使BG=BE，連接EG，若∠B=∠FED=60°，求證：；EFED=BECD
（3）如圖3，若∠ABC=90°，點C關于BD的對稱點為點C'，CC′交BD于點M，對角線AC、BD交于點O，連接OC'交AD于點G，求AG的長．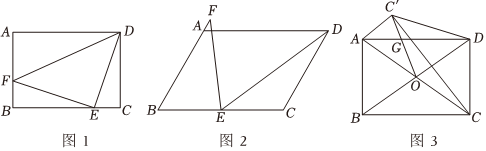
發布：2025/5/24 14:30:1組卷：496引用：4難度：0.1 -
3．（1）問題發現
如圖1，在△OAB和△OCD中，OA=OB，OC=OD，∠AOB=∠COD=40°，連接AC，BD交于點M，填空：的值為；∠AMB的度數為，ACBD
（2）類比探究
如圖2，在△OAB和△OCD中，∠AOB=∠COD=90°，∠OAB=∠OCD=30°，連接AC交BD的延長線于點M，請判斷的值及∠AMB的度數，并說明理由．ACBD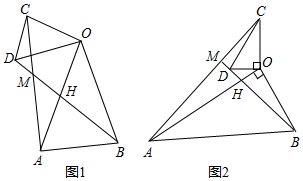
發布：2025/5/24 12:30:1組卷：917引用：7難度：0.3