用如圖1所示的曲尺形框框(有三個方向),可以套住圖2日歷中的三個數,設被框住的三個數中(第一個框框住的最大的數為a;第二個框框住的最大的數為b;第三個框框住的最大的數為c).
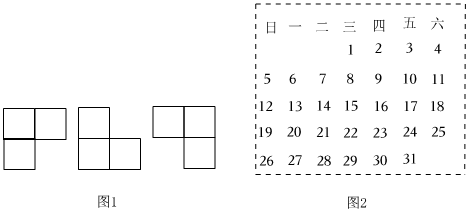
(1)第一個框框住的三個數的和是:3a-133a-13,第二個框框住的三個數的和是:3b-93b-9,
第三個框框住的三個數中的和是:3c-153c-15;
(2)這三個框框住的數的和分別能等于81嗎?若能,請分別求出最大的數a、b、c;若不能,請分別說明理由.
【考點】一元一次方程的應用;規律型:數字的變化類.
【答案】3a-13;3b-9;3c-15
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2025/6/2 16:0:1組卷:19引用:1難度:0.6
相似題
-
1.如圖,已知數軸上有A、B、C三點,點O為原點,點A、點B在原點的右側,點C在原點左側,點A表示的數為a,點B表示的數為b,且a與b滿足|a-4|+(b-10)2=0,AC=24.
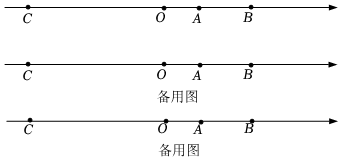
(1)直接寫出a、b的值,a=,b=;
(2)動點P從點C出發,以每秒6個單位的速度沿數軸的正方向運動,同時動點Q從點B出發,以每秒3個單位的速度沿數軸的正方向運動,設運動時間為t(t>0)秒,請用含t的式子表示線段PQ的長度;
(3)在(2)的條件下,若點M為AP的中點,點R為PQ的中點,求t為何值時,滿足2MO=MR.發布:2025/6/4 9:0:1組卷:261引用:2難度:0.5 -
2.某同學把積攢的零用錢1000元存入銀行,月利率是0.24%,如果到期他連本帶利可取回1024元,那么他共存了個月.
發布:2025/6/3 21:30:1組卷:159引用:4難度:0.8 -
3.小明、小麗分別在400米環形跑道上練習跑步與競走,小明每分鐘跑200米,小麗每分鐘走80米,兩人由同一起點同向出發,小麗先走了3分鐘后,小明才出發.
(1)小明出發幾分鐘后與小麗第一次相遇?
(2)若小明與小麗第二次相遇時小明和小麗同時結束跑步與競走,那么小明出發幾分鐘后與小麗相距100米?(直接寫出結果)發布:2025/6/3 22:0:1組卷:239引用:2難度:0.7


