閱讀下面材料:
數學課上,老師給出了如下問題:
如圖,AD為△ABC中線,點E在AC上,BE交AD于點F,AE=EF.求證:AC=BF.

經過討論,同學們得到以下兩種思路:
思路一如圖①,添加輔助線后依據SAS可證得△ADC≌△GDB,再利用AE=EF可以進一步證得∠G=∠FAE=∠AFE=∠BFG,從而證明結論. |
思路二如圖②,添加輔助線后并利用AE=EF可證得∠G=∠BFG=∠AFE=∠FAE,再依據AAS可以進一步證得△ADC≌△GDB,從而證明結論. |
(1)①思路一的輔助線的作法是:
延長AD至點G,使DG=AD,連接BG
延長AD至點G,使DG=AD,連接BG
;②思路二的輔助線的作法是:
作BG=BF交AD的延長線于點G
作BG=BF交AD的延長線于點G
.(2)請你給出一種不同于以上兩種思路的證明方法(要求:只寫出輔助線的作法,并畫出相應的圖形,不需要寫出證明過程).
【考點】全等三角形的判定與性質.
【答案】延長AD至點G,使DG=AD,連接BG;作BG=BF交AD的延長線于點G
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:1982引用:3難度:0.5
相似題
-
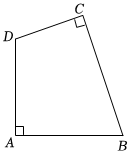 1.如圖,已知四邊形ABCD中,∠A=∠C=90°,AB=AD,四邊形ABCD的面積是8,有如下結論:①∠B+∠D=180°,②BC=2,③AC=4,④BC+CD=42,其中一定正確的是( )2
1.如圖,已知四邊形ABCD中,∠A=∠C=90°,AB=AD,四邊形ABCD的面積是8,有如下結論:①∠B+∠D=180°,②BC=2,③AC=4,④BC+CD=42,其中一定正確的是( )2
?A.①② B.①②③ C.①③④ D.②③④ 發布:2025/6/4 18:30:2組卷:123引用:1難度:0.3 -
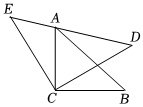 2.如圖,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的頂點A在△ECD的斜邊DE上,求證:AE2+AD2=2AC2.發布:2025/6/4 19:0:1組卷:920引用:8難度:0.3
2.如圖,△ACB和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ACB的頂點A在△ECD的斜邊DE上,求證:AE2+AD2=2AC2.發布:2025/6/4 19:0:1組卷:920引用:8難度:0.3 -
 3.如圖,△ABC中,∠C=90°,點D在BC上,且DE⊥AB于點E,AE=AC,若BC=4,DE=1.5,則BD=.發布:2025/6/4 18:30:2組卷:173引用:1難度:0.6
3.如圖,△ABC中,∠C=90°,點D在BC上,且DE⊥AB于點E,AE=AC,若BC=4,DE=1.5,則BD=.發布:2025/6/4 18:30:2組卷:173引用:1難度:0.6


