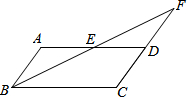
我們知道：平行四邊形的面積=（底邊）×（這條底邊上的高）．如圖，四邊形ABCD都是平行四邊形，AD∥BC，AB∥CD，設它的面積為S．
（1）如圖①，點M為AD上任意一點，若△BCM的面積為S₁，則S₁：S=
1：2
1：2
；
（2）如圖②，點P為平行四邊形ABCD內任意一點時，記△PAB的面積為Sˊ，△PCD的面積為S″，平行四邊形ABCD的面積為S，猜想得Sˊ、S″的和與S的數量關系式為
Sˊ+S″=
1
2
S
Sˊ+S″=
1
2
S
；
（3）如圖③，已知點P為平行四邊形ABCD內任意一點，△PAB的面積為3，△PBC的面積為7，求△PBD的面積．

【答案】1：2；Sˊ+S″=

【解答】

【點評】

聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。

發布：2024/6/27 10:35:59組卷：928引用：3難度：0.3

相似題

1．如圖，?ABCD在平面直角坐標系中，點A、B分別在x軸和y軸負半軸上，OA=OB=2，點C的坐標為（4，0），求點D的坐標．
?
發布：2025/5/21 23:0:1組卷：140引用：1難度：0.6
解析
2．如圖，平行四邊形ABCD中，點E是AD的中點，連接BE并延長交CD的延長線于點F．求證：△ABE≌△DFE．
發布：2025/5/22 0:0:2組卷：268引用：3難度：0.7
解析
3．如圖，點E，F分別是?ABCD的邊AD，BC的中點，連接BF，DE．求證：BE=DF．
發布：2025/5/22 0:30:1組卷：70引用：1難度：0.6
解析

相關試卷

1．如圖，?ABCD在平面直角坐標系中，點A、B分別在x軸和y軸負半軸上，OA=OB=2，點C的坐標為（4，0），求點D的坐標．?