三角形中有三條重要線段——中線，高線和角平分線，下面我們一起來研究中線和高線的特點．
問題1：如圖1：AD是△ABC的中線，求證：S△ABD=S△ACD．
問題2：如圖2：AD∥BC，求證：S△ABC=S△BCD．
問題3：運用上述兩個問題的發現我們一起探究如何作一條直線平分多邊形面積：
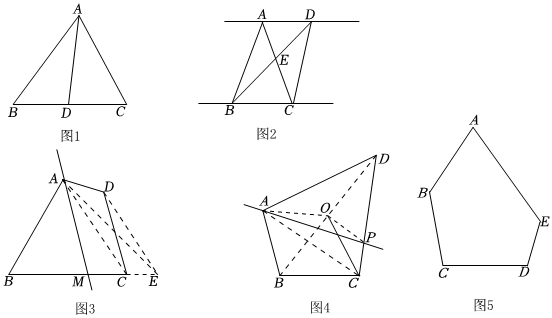
（1）如圖3：在四邊形ABCD，小孫同學的輔助線：
①連接對角線AC；
②作DE∥AC交BC的延長線于E；
③取BE的中點M，則直線AM為所求直線．
（2）如圖4：在四邊形ABCD，小悟同學的輔助線：
①連接對角線AC和BD；
②取BD的中點O；
③連接OA、OC；
④過點O作AC的平行線與四邊形ABCD的邊CD交點于P，則直線AP則為所求直線．
下面就請你完成小孫和小悟的證明．
問題4：小空同學運用類比和轉化的數學思想作了一條直線平分五邊形ABCDE，請你也嘗試畫一畫吧！（保留作圖痕跡并寫出作圖方法）
【考點】四邊形綜合題．
【答案】小孫的理由：見解析過程；
小悟的理由：見解析過程；
問題4：見解析過程．
小悟的理由：見解析過程；
問題4：見解析過程．
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：434引用：2難度：0.3
相似題
-
1．定義：只有一組對角是直角的四邊形叫做損矩形，連接它的兩個非直角頂點的線段叫做這個損矩形的直徑．如圖1，∠ABC=∠ADC=90°，四邊形ABCD是損矩形，則該損矩形的直徑是線段AC．同時我們還發現損矩形中有公共邊的兩個三角形角的特點：在公共邊的同側的兩個角是相等的．如圖1中：△ABC和△ABD有公共邊AB，在AB同側有∠ADB和∠ACB，此時∠ADB=∠ACB；再比如△ABC和△BCD有公共邊BC，在CB同側有∠BAC和∠BDC，此時∠BAC=∠BDC．
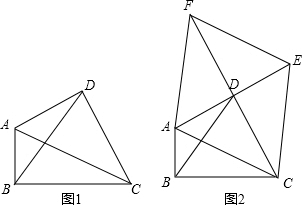
（1）請在圖1中再找出一對這樣的角來：=．
（2）如圖2，△ABC中，∠ABC=90°，以AC為一邊向外作菱形ACEF，D為菱形ACEF對角線的交點，連接BD，當BD平分∠ABC時，判斷四邊形ACEF為何種特殊的四邊形？請說明理由．
（3）在第（2）題的條件下，若此時AB=6，BD=8，求BC的長．2發布：2025/6/8 10:0:2組卷：584引用：6難度：0.3 -
2．如圖，在長方形OABC中，O為平面直角坐標系的原點，點A坐標為（a,0），點C的坐標為（0，b），且a、b滿足+|b-8|=0，點B在第一象限內，點P從原點出發，以每秒2個單位長度的速度沿著O-C-B-A-O的線路移動．a-4
（1）求a,b的值，點B的坐標．
（2）當點P移動4.5秒時，請指出點P的位置，并求出點P的坐標；
（3）在O-C-B段的移動過程中，當△OPB的面積是12時，求點P移動的時間．發布：2025/6/8 9:30:1組卷：123引用：3難度：0.1 -
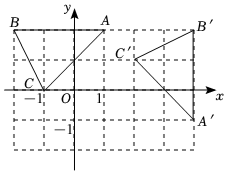3．如圖，在平面直角坐標系中，△ABC繞旋轉中心順時針旋轉90°后得到△A'B'C'，
（1）其旋轉中心的坐標是 ；
（2）寫出點C掃過的路徑長 ；
（3）若在平面內有一點D，且四邊形ABCD是平行四邊形，則該四邊形的周長為 ；
（4）在坐標軸上有點E，使S△ABC=S△AEC，直接寫出E點坐標 （寫出平面內所有符合條件的點坐標）．發布：2025/6/8 10:0:2組卷：81引用：2難度：0.3