綜合與探究,問題情境:
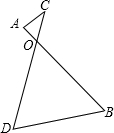
如圖1,已知AB∥CD,∠ABC=60°,∠BAD=120°,點E,F在直線AB上,且∠ACD=∠ACF,CE平分∠BCF.

(1)求∠ACE的度數.
實踐探究:
(2)若左右平行移動AD,那么∠BAC與∠BFC之間的數量關系是否發生變化?若變化,請說明理由;若不變,請求出∠BAC與∠BFC之間的數量關系.
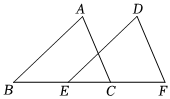
(3)如圖2,若向左平行移動AD,當∠BEC=∠CAD時,請求出∠CAD的度數.
【答案】(1)60°;
(2)∠BFC=2∠BAC,理由見解析;
(3)90°.
(2)∠BFC=2∠BAC,理由見解析;
(3)90°.
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/7/5 8:0:9組卷:268引用:3難度:0.5