問題提出：
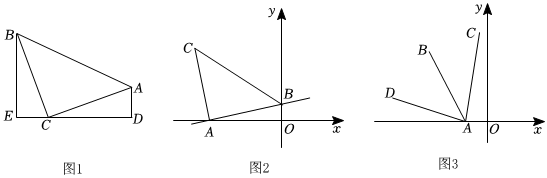
如圖，等腰Rt△ABC中，∠ACB=90°，CB=CA，直線ED經過點C，過點A作AD⊥ED于點D，過點B作BE⊥ED于點E，求證：△BEC≌△CDA；
問題探究：
如圖2，在平面直角坐標系中，一次函數y=15x+1與x軸交于點A，與y軸交于點B，以AB為腰在第二象限作等腰直角△ABC，∠BAC=90°，求點C的坐標；
問題解決：
古城西安已經全面迎來地鐵時代！繼西安地鐵2號線于2011年9月16日通車試運行以來，共有八條線路開通運營，極大促進了西安市的交通運輸，目前還有多條線路正在修建中．如圖，地鐵某線路原計劃按OA-AB的方向施工，由于在AB方向發現一處地下古建筑，地鐵修建須繞開此區域．經實地勘測，若將AB段繞點A順時針或逆時針方向旋轉45°至AC或AD方向，則可以繞開此區域．已知OA長為1千米，以點O為原點，OA所在直線為x軸，1千米為單位長度，建立平面直角坐標系，且射線AB與直線y=-2x平行，請幫助施工隊計算出AC和AD所在直線的解析式．
y
=
1
5
x
+
1
【考點】一次函數綜合題．
【答案】問題提出：見解析；問題探究：C（-6，5）；問題解決：直線AC：y=3x+3；直線AD：．
y
=
-
1
3
x
-
1
3
【解答】
【點評】
聲明：本試題解析著作權屬菁優網所有，未經書面同意，不得復制發布。
發布：2024/6/27 10:35:59組卷：292引用：3難度：0.2
相似題
-
1．如圖1，在平面直角坐標系中，直線l1：y=kx+3與直線l2：y=-x-6交于點A，已知點A的橫坐標為
，直線l1與x軸交于點B，與y軸交于點C，直線l2與x軸交于點F，與y軸交于點D．-185
（1）求直線l1的解析式；
（2）將直線l2向上平移個單位得到直線l3，直線l3與y軸交于點E，過點E作y軸的垂線l4，若點M為垂線l4上的一個動點，點N為l2上的一個動點，求DM+MN的最小值；92
（3）已知點P、Q分別是直線l1、l2上的兩個動點，連接EP、EQ、PQ，是否存在點P、Q，使得△EPQ是以點Q為直角頂點的等腰直角三角形，若存在，求點Q的坐標；若不存在，說明理由．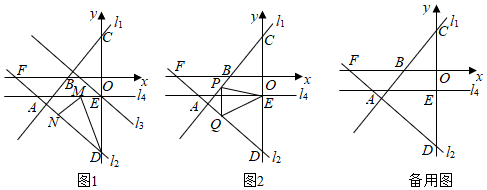
發布：2025/6/21 23:30:2組卷：566引用：2難度：0.2 -
2．如圖1，在平面直角坐標系中，直線l1：y=-
x+333與x軸相交于B，與y軸相交于點A．直線l2：y=3x經過原點，并且與直線l1相交于C點．33
（1）求△OBC的面積；
（2）如圖2，在x軸上有一動點E，連接CE．問CE+BE是否有最小值，如果有，求出相應的點E的坐標及CE+12BE的最小值；如果沒有，請說明理由；12
（3）如圖3，在（2）的條件下，以CE為一邊作等邊△CDE，D點正好落在x軸上，將△DCE繞點D順時針旋轉，旋轉角度為α（0°≤α≤180°），記旋轉后的三角形為△DC'E′，點C，E的對稱點分別為C'，E′．在旋轉過程中，設C'E'所在的直線與直線l1相交于點M，與x軸正半軸相交于點N．當△BMN為等腰三角形時，求旋轉角α的度數？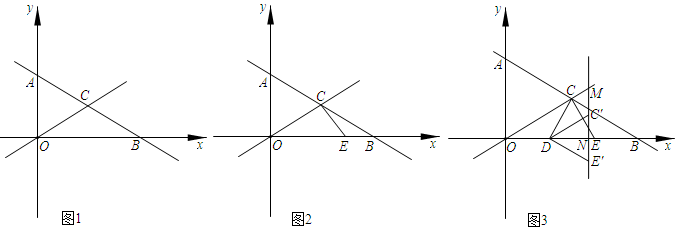
發布：2025/6/21 23:30:2組卷：631引用：1難度：0.3 -
3．已知：如圖，在平面直角坐標系中，△ABC為直角三角形，∠B=90°，∠A=30°，點C的坐標為（1，0），點B的坐標為（0，
），EF垂直平分AC，交AB于點E，交x軸于點F．3
（1）求點E的坐標；
（2）點P從點C出發沿射線CB以每秒1個單位的速度運動，設點P運動的時間為t秒，設△PBE的面積為S，用含t的代數式表示S，并直接寫出t的取值范圍；
（3）在（2）的條件下，過點F作直線m∥BC，在直線m上是否存在點Q，使得△PFQ為等腰直角三角形？若存在，求滿足條件t的值，并直接寫出Q的坐標；若不存在，請說明理由．
發布：2025/6/21 23:30:2組卷：177引用：2難度：0.3