2022-2023學年廣東省梅州市豐順縣三友中學八年級（下）開學數學試卷

一、單選題：本大題共10小題，每小題3分，共30分。

• 1．若分式

  |

  x

  |

  -

  1

  x

  +

  1

  的值為零，則x的值是（　　）

  A．1

  B．-1

  C．±1

  D．2
  組卷：4770引用：40難度：0.7

  解析

• 2．對于①a-2ab=a（1-2b），②（a+2）（a-1）=a²+a-2，從左到右的變形，表述正確的是（　　）

  A．①是因式分解，②是乘法運算

  B．①是乘法運算，②是因式分解

  C．①②都是因式分解

  D．①②都是乘法運算
  組卷：178引用：4難度：0.8

  解析

• 3．已知x=-2時，分式

  x

  -

  1

  □

  無意義，則□可以是（　　）

  A．2-x

  B．x-2

  C．2x+4

  D．x+4
  組卷：1606引用：11難度：0.9

  解析

• 4．周末李強和朋友到森林公園游玩，為測量園內湖岸A，B兩點之間的距離，如圖，李強在湖的一側選取了一點O，測得OA=20m,OB=8m,則A，B間的距離可能是（　　）

  A．10m

  B．22m

  C．30m

  D．32m
  組卷：294引用：7難度：0.6

  解析

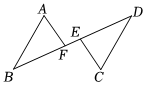• 5．如圖，已知BF=DE，AB∥DC，要使△ABF≌△CDE，添加的條件可以是（　　）

  A．BE=DF

  B．AF=CE

  C．AB=CD

  D．∠B=∠D
  組卷：211引用：6難度：0.7

  解析

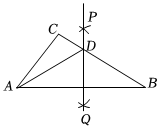• 6．如圖，在△ABC中，分別以點A和點B為圓心，大于

  1

  2

  AB的長為半徑畫弧，兩弧相交于點P、Q，作直線PQ交AB于點D，連接AD，若△ABC的周長為15，AB=6，則△ADC的周長為（　　）

  A．6

  B．7

  C．8

  D．9
  組卷：100引用：4難度：0.6

  解析

• 7．在△ABC中，AB=2，BC=3，AC的長不可能的是（　　）

  A．1

  B．2

  C．3

  D．4
  組卷：134引用：2難度：0.7

  解析

• 8．已知Rt△ABC≌Rt△EDF，Rt△ABC的面積為12，Rt△EDF的一條直角邊等于3，則另一直角邊的長是（　　）

  A．2

  B．4

  C．6

  D．8
  組卷：166引用：4難度：0.7

  解析

三、解答題：第18，19.20小題6分，第21，22，23小題9分，第24，25小題10分。

• 24．問題提出：
  如圖，等腰Rt△ABC中，∠ACB=90°，CB=CA，直線ED經過點C，過點A作AD⊥ED于點D，過點B作BE⊥ED于點E，求證：△BEC≌△CDA；
  問題探究：
  如圖2，在平面直角坐標系中，一次函數

  y

  =

  1

  5

  x

  +

  1

  與x軸交于點A，與y軸交于點B，以AB為腰在第二象限作等腰直角△ABC，∠BAC=90°，求點C的坐標；
  問題解決：
  古城西安已經全面迎來地鐵時代！繼西安地鐵2號線于2011年9月16日通車試運行以來，共有八條線路開通運營，極大促進了西安市的交通運輸，目前還有多條線路正在修建中．如圖，地鐵某線路原計劃按OA-AB的方向施工，由于在AB方向發現一處地下古建筑，地鐵修建須繞開此區域．經實地勘測，若將AB段繞點A順時針或逆時針方向旋轉45°至AC或AD方向，則可以繞開此區域．已知OA長為1千米，以點O為原點，OA所在直線為x軸，1千米為單位長度，建立平面直角坐標系，且射線AB與直線y=-2x平行，請幫助施工隊計算出AC和AD所在直線的解析式．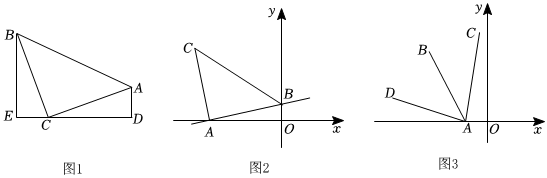
  
  組卷：292引用：3難度：0.2

  解析

• 25．小明在學習過程中，對教材中的一個有趣問題做如下探究：
  
  【習題回顧】已知：如圖1，在△ABC中，∠ACB=90°，AE是角平分線，CD是高，AE、CD相交于點F．求證：∠CFE=∠CEF；
  【變式思考】如圖2，在△ABC中，∠ACB=90°，CD是AB邊上的高，若△ABC的外角∠BAG的平分線交CD的延長線于點F，其反向延長線與BC邊的延長線交于點E，則∠CFE與∠CEF還相等嗎？說明理由；
  【探究延伸】如圖3，在△ABC中，在AB上存在一點D，使得∠ACD=∠B，角平分線AE交CD于點F．△ABC的外角∠BAG的平分線所在直線MN與BC的延長線交于點M．試判斷∠M與∠CFE的數量關系，并說明理由．
  組卷：7892引用：21難度：0.3

  解析