在△ABC中，∠ACB=90°，CA=CB，點(diǎn)D為線段CB上一點(diǎn)，連接AD，將線段AD繞著點(diǎn)A逆時(shí)針旋轉(zhuǎn)α（0°＜α＜90°）得到線段AD'，延長AD'交CB延長線于點(diǎn)E．
（1）如圖1，當(dāng)點(diǎn)D與點(diǎn)C重合時(shí)，連接CD'，若AC=3，D'E=2，求線段CD'的長；
（2）如圖2，當(dāng)α=45°時(shí)，過點(diǎn)B作BF⊥BC交AE于點(diǎn)F，過點(diǎn)F作FG⊥AC，垂足為點(diǎn)G，AD與FG交于點(diǎn)H，求證：CD=BF-GH；
（3）如圖3，當(dāng)點(diǎn)D與點(diǎn)B重合且α=30°時(shí)，將△D'AB沿著AB邊翻折到同一平面內(nèi)得到△D″AB，點(diǎn)P、點(diǎn)Q分別為線段AB、線段AD″上的動點(diǎn)，且AP=D″Q，連接D′Q，PD″，當(dāng)D′Q+PD″取得最小值時(shí)，請直接寫出AD′PQ的值．
AD
′
PQ
【考點(diǎn)】幾何變換綜合題．
【答案】（1）；
（2）證明見解析部分；
（3）．
6
5
5
（2）證明見解析部分；
（3）
2
+
6
2
【解答】
【點(diǎn)評】
聲明：本試題解析著作權(quán)屬菁優(yōu)網(wǎng)所有，未經(jīng)書面同意，不得復(fù)制發(fā)布。
發(fā)布：2024/6/27 10:35:59組卷：587引用：1難度：0.1
相似題
-
1．綜合與實(shí)踐
“手拉手”模型是初中幾何圖形的一種全等變形的重要模型，可以借助旋轉(zhuǎn)和全等形的相關(guān)知識結(jié)合勾股定理等，來解決有關(guān)線段的長、角的度數(shù)等問題，在學(xué)習(xí)和生活中應(yīng)用廣泛，有著十分重要的地位和作用．
某校數(shù)學(xué)活動小組進(jìn)行了有關(guān)旋轉(zhuǎn)的系列探究：
如圖①，已知△ABC和△ADE均是等腰直角三角形，∠BAC=∠DAE=90°，且AB=AC，AD=AE，易證：BD=CE，BD⊥CE．
深入探究：
（1）如圖②，將圖①中△ABC繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)α（0°＜α＜90°），連接BD、CE，并延長CE分別與AB、BD相交于點(diǎn)G、F，求證：BD=CE，BD⊥CE．
解決問題：
（2）如圖③，將圖①中△ABC繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)90°，使AE與AB重合，其他條件不變，若AB=6，AD=3，則CE=，DF=．
拓展應(yīng)用：
（3）如圖④，將圖①中△ABC繞點(diǎn)A逆時(shí)針旋轉(zhuǎn)α（90°＜α＜180°），連接BD、CE，若AB=4，BE=3，∠ABE=45°，則BD=，AD=．2
（提示：求AD時(shí)，可過點(diǎn)E作EH⊥AB于點(diǎn)H）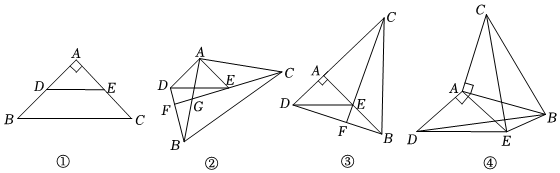
發(fā)布：2025/5/25 7:30:1組卷：887引用：2難度：0.2 -
2．如圖1，在△ABC中，∠C=90°，∠ABC=30°，AC=1，D為△ABC內(nèi)部的一動點(diǎn)（不在邊上），連接BD，將線段BD繞點(diǎn)D逆時(shí)針旋轉(zhuǎn)60°，使點(diǎn)B到達(dá)點(diǎn)F的位置；將線段AB繞點(diǎn)B順時(shí)針旋轉(zhuǎn)60°，使點(diǎn)A到達(dá)點(diǎn)E的位置，連接AD，CD，AE，AF，BF，EF．
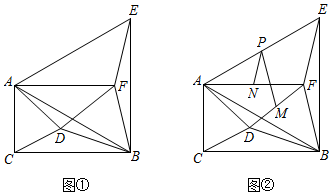
（1）求證：△BDA≌△BFE；
（2）①CD+DF+FE的最小值為 ；
②當(dāng)CD+DF+FE取得最小值時(shí)，求證：AD∥BF．
（3）如圖2，M，N，P分別是DF，AF，AE的中點(diǎn)，連接MP，NP，在點(diǎn)D運(yùn)動的過程中，請判斷∠MPN的大小是否為定值．若是，求出其度數(shù)；若不是，請說明理由．發(fā)布：2025/5/25 8:0:2組卷：2338引用：3難度：0.5 -
3．如圖，已知△ABC和△ADE均為等腰三角形，AC=BC，DE=AE，將這兩個三角形放置在一起．
（1）問題發(fā)現(xiàn)：
如圖①，當(dāng)∠ACB=∠AED=60°時(shí)，點(diǎn)B、D、E在同一直線上，連接CE，則線段BD、CE之間的數(shù)量關(guān)系是，∠CEB=°；
（2）拓展探究：
如圖②，當(dāng)∠ACB=∠AED=α?xí)r，點(diǎn)B、D、E不在同一直線上，連接CE，求出線段BD、CE之間的數(shù)量關(guān)系及BD、CE所在直線相交所成的銳角的大小（都用含α的式子表示），并說明理由；
（3）解決問題：
如圖③，∠ACB=∠AED=90°，AC=，AE=10，連接CE、BD，在△AED繞點(diǎn)A旋轉(zhuǎn)的過程中，當(dāng)CE所在的直線垂直于AD時(shí)，請你直接寫出BD的長．2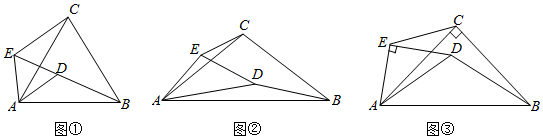
發(fā)布：2025/5/25 4:30:1組卷：1343引用：2難度：0.1
相關(guān)試卷