 閱讀與應用
閱讀與應用
我們知道(a-b)2≥0,即a2-2ab+b2≥0,所以a2+b2≥2ab(當且僅當a=b時取等號).
| 閱讀1:若a,b為實數, 且a>0,b>0,∵ ( a - b ) 2 ≥ 0 a - 2 ab + b ≥ 0 a + b ≥ 2 ab |
閱讀2:若函數 y = x + m x 由閱讀1的結論可知 x + m x ≥ 2 x ? m x x + m x ≥ 2 m x = m x y = x + m x 2 m |
(1)當x=
2
2
時,函數y
=
x
+
4
x
(
x
>
0
)
4
4
.(2)疫情防控期間,某核酸檢測采樣點用隔離帶分區管理,如圖是一邊靠墻其它三邊用隔離帶圍成的面積為32m2的矩形隔離區域,假設墻足夠長,則這個矩形隔離區域的長和寬分別是多少時,所用隔離帶的長度最短?
(3)隨著高科技賦能傳統快遞行業,某大型物流公司為提高工作效率引進一批分揀機器人,已知每臺機器人的運營成本包含以下三個部分:一是進價為25000元;二是材料損耗費,每小時為7元;三是折舊費,折舊費y(元)與運營工作時間t(小時)的函數關系式為y=0.1t2(t>0).當運營工作時間t長達多少小時時,每臺機器人平均每小時的運營成本最低?最低運營成本是多少?
【考點】二次函數的應用.
【答案】2;4
【解答】
【點評】
聲明:本試題解析著作權屬菁優網所有,未經書面同意,不得復制發布。
發布:2024/6/27 10:35:59組卷:422引用:3難度:0.2
相似題
-
1.2022年2月8日北京冬奧會中自由滑雪空中技巧項目備受大家關注,中國優秀運動員沿跳臺斜坡AB加速加速至B處騰空而起,沿拋物線BEF運動,在空中完成翻滾動作,著陸在跳臺的背面著陸坡DC.建立如圖所示的平面直角坐標系,BD∥x軸,C在x軸上,B在y軸上,已知跳臺的背面DC近似是拋物線y=a(x-7)2(1≤x≤7)的一部分,D點的坐標為(1,6),拋物線BEF的表達式為y=b(x-2)2+k.
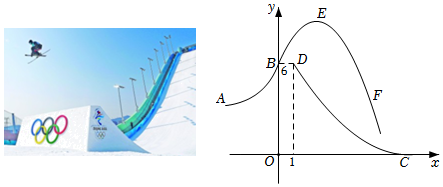
(1)當k=10時,求a、b的值;
(2)在(1)的條件下,運動員在離x軸3.75m處完成動作并調整好身姿,求此時他距DC的豎直距離(豎直距離指的是運動員所在位置的點向x軸的垂線與DC的交點之間線段的長);
(3)若運動員著落點與B之間的水平距離需要在不大于7m的位置(即著落點的橫坐標x滿足x≤7且b<0,),求b的取值范圍.發布:2024/12/23 13:30:1組卷:357引用:4難度:0.4 -
2.如圖1,某公園在入園處搭建了一道“氣球拱門”,拱門兩端落在地面上.若將拱門看作拋物線的一部分,建立如圖2所示的平面直角坐標系.拱門上的點距地面的豎直高度y(單位:m)與水平距離x(單位:m)近似滿足函數關系y=a(x-h)2+k(a<0).
(1)拱門上的點的水平距離x與豎直高度y的幾組數據如下:
根據上述數據,直接寫出“門高”(拱門的最高點到地面的距離),并求出拱門上的點滿足的函數關系y=a(x-h)2+k(a<0).水平距離x/m 2 3 6 8 10 12 豎直高度y/m 4 5.4 7.2 6.4 4 0
(2)一段時間后,公園重新維修拱門.新拱門上的點距地面的豎直高度y(單位:m)與水平距離x(單位:m)近似滿足函數關系y=-0.288(x-5)2+7.2,若記“原拱門”的跨度(跨度為拱門底部兩個端點間的距離)為d1,“新拱門”的跨度為d2,則d1d2(填“>”“=”或“<”).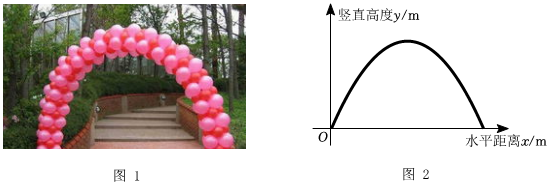 發布:2024/12/23 11:30:2組卷:581引用:6難度:0.5
發布:2024/12/23 11:30:2組卷:581引用:6難度:0.5 -
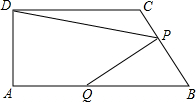 3.如圖,已知梯形ABCD中,DC∥AB,∠A=90°,∠B=60°,AD=3,AB=,DC=53,P是BC邊上一點(P與B不重合),過點P作PQ⊥BC交AB于Q,設PB=x,四邊形AQPD的面積為y.43
3.如圖,已知梯形ABCD中,DC∥AB,∠A=90°,∠B=60°,AD=3,AB=,DC=53,P是BC邊上一點(P與B不重合),過點P作PQ⊥BC交AB于Q,設PB=x,四邊形AQPD的面積為y.43
(1)求y與x的函數關系式;
(2)當x為何值時,y有最大值或最小值?其值等于多少?發布:2025/1/21 8:0:1組卷:31引用:1難度:0.5


